Search

What is the weight of Earth's atmosphere? What percentage of weight does it make up? For the purposes of this problem you know only the mass of the Earth $M_{Z}$ and the radius $R_{Z}$ Zeme, gravitational acceleration $a_{g}$ on the surface of the Earth, density of water $ρ$ and you know that near the surface of the Earth at the depth of $h_{1}=10\;\mathrm{m}$ it has the pressure of approximately one atmosphere $p_{a}=10^{5}Pa$.

Hint: It is a simple task. We don't want a perfect solution but a qualified estimation.

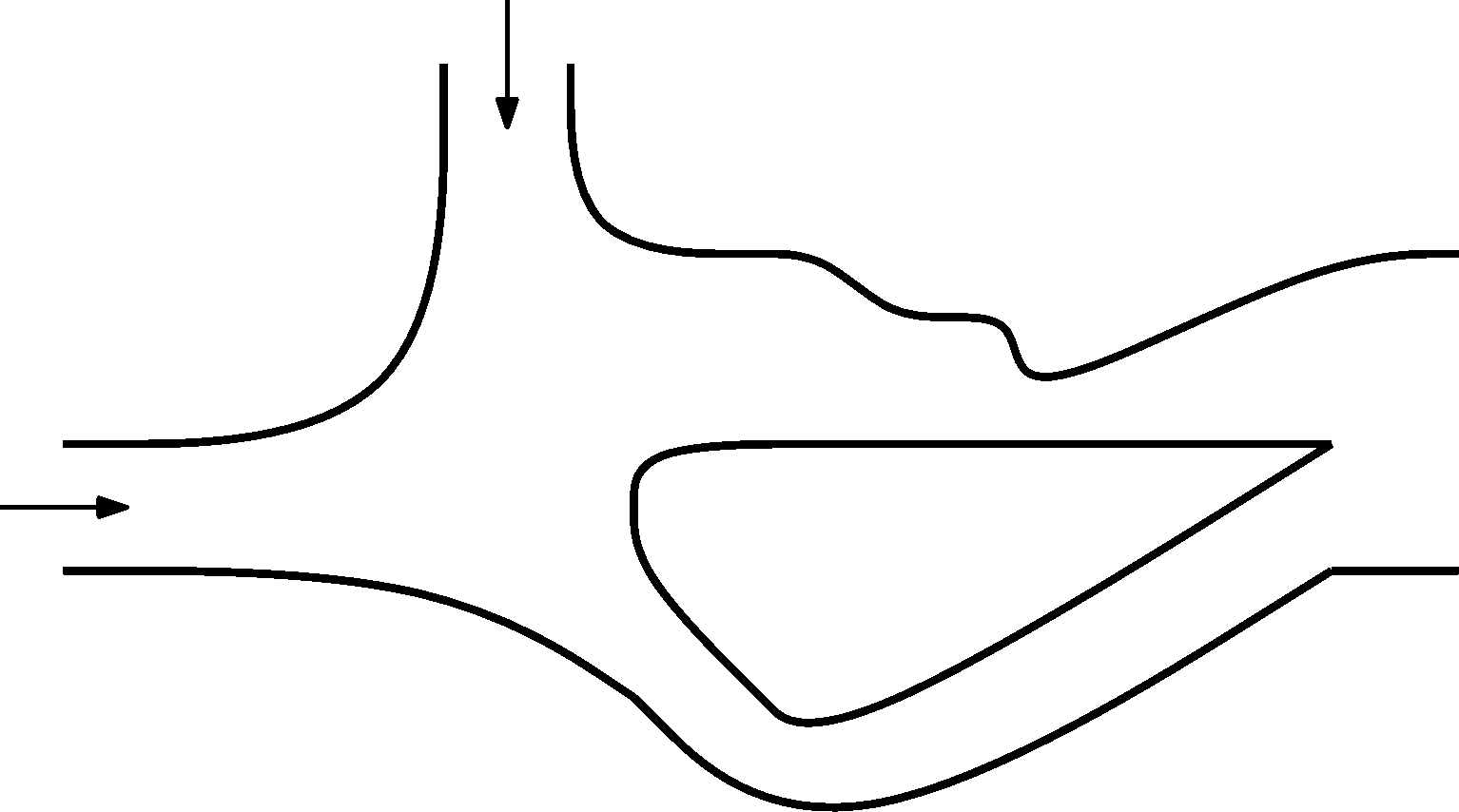
Draw streamlines into the picture. Into both openings with an arrow the same amount of water flows, All the water then flows out through one opening, the third one. The flow is stable and is slow enough that we can consider it not to be turbulent. When drawing follow the rules that dictate the shapes of the streamlines and write these rules down as comments to the picture. We don't expect that this problem will be solved quantitatively. Comment Draw into the bigger picture available from the website.

Explain why and how the following situations occur:

• In a cistern of a rectangular cuboid shape that is filled with water a ball is floating on the surface of the water. Describe the movement of the ball if the cistern starts moving with a constant acceleration small enough that the water shall not flow over the edge.
• In a cistern of a rectangular cuboid shape that is filled with water a ball filled with water is floating. Describe the movement of the ball if the cistern starts moving with a constant acceleration small enough that the water shall not flow over the edge.
• In a closed bus a ballon is floating near the ceiling. Describe its movement if the bus starts accelerating constantly

Náry always wanted a boat and so one beautiful day he bought himself one in the shape of a cuboid without a top side (like a bath) with outer sides of $a$, $b$, $c$ and with a width of wall of $d$, which was created from scented wood of a density $ρ$ (bigger density than water). The second day he took his boat outfor a ride on the water and he found out that it has a small hole on the bottom through which water flows with a flow rate of $Q_{1}$. That was unfortunate but since he was a man of action he started calculating how long until water starts entering the boat from the top. The same question is asked by this task.Conider also the situation where Náry of a mass $m$ would have sat in the boat and while calculating would spill water out of the boat with a flow rate of $Q_{2}$. The boat is horizontal the whole time.

Compare the blood pressure in the head of an adult giraffe and an adult human $p_{h1}=120\;\mathrm{mm}Hg$ and in the giraffe $p_{g1}=280\;\mathrm{mm}Hg,the$ density of the blood of both animals is $ρ=1050\;\mathrm{kg}\cdot m$. Consider only the case where both the human and giraffe are standing. The speed of the flow of the blood is to be assumed constant.

Test tubes of volumes 3 ml and 5 ml are connected by a short thin tube in which we can find a porous thermally non-conductive barrier that allows an equilbirum in pressures to be achieved within the system. Both test tubes in the beginning are filled with oxygen at a pressure of 101,25 kPa and a temperature of 20 ° C. We submerge the first test tube (3 ml) into a container which has a system of water and ice in equilbrium inside it and the other one (5 ml) into a container with steam. What wil the pressure be in the system of the teo test tubes be after achieving mechanical equilibrium? What would the pressure be if it would have been nitrogen and not oxygen that was in the test tubes?(while keeping other conditions the same)/p>

How quickly on average does water flow through the Gibralatar Strait if it allows the changing of high and low tide in the Mediteranean Sea? Find the required data on the internet and don't forget to cite them properly!

Take an empty cylindrical cup. Turn it upside down and push it beneath a calm water surface. How high will the column of air in the cup be depending on the submersion of the cup?

A hot air balloon with its basket weighs $M$. The basket of the baloon is submerged into a water reservoir and water flows into it. Now we shall raise the temperature a bit and by that we raise the buoyant force acting on the balloon $Mg+F$. The basket has the shape of a rectangular cuboid with a square base which has a side of size $a$ and is submerged into a depth $H$. The openings in the basket make up $p≪1$ of the whole area of the basket about which we assume that it is empty (with the exception of water). Let us neglect the viscosity of water and the volume of the basket itself. How quickly shall it rise depending on the depth of submersion?

Bonus: When shall it emerge?

Tip The expected speed of water flowing from the basket above the water surface is 2/3 of the maximum speed of water flowing out.

Each liquid has its specific viscosity. Try to make an Ostwald viscometer (capillary viscometer) and measure the relative viscosity of a few (at least three) liquids compared to water. Compare your results with what you find online.