Search
astrophysics (85)biophysics (18)chemistry (23)electric field (70)electric current (75)gravitational field (80)hydromechanics (146)nuclear physics (44)oscillations (56)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (295)gas mechanics (87)mechanics of rigid bodies (220)molecular physics (71)geometrical optics (77)wave optics (65)other (164)relativistic physics (37)statistical physics (21)thermodynamics (153)wave mechanics (51)
mathematics
(6 points)1. Series 30. Year - 4. The world is tilted
An observer is on a ship in the open sea, in the height $h$ above the sea surface. There is a horizontal railing in the distance $d$ from him, in such a position, that when he looks directly, perpendicularly at it, the bottom edge of the railings touches the horizon. However, when he looks at the part of the railing that is distance $l$ to the left of the original point, the horizon appears to be $s±s_{s}$ lower. What is the radius of the Earth.
Lubošek trpí mořskou nemocí.
(7 points)1. Series 30. Year - 5. On a walk
Katka decided to go for a walk with her pet rat. They arrived on a flat meadow and when the rat was at a distance $x_{1}=50\;\mathrm{m}$ from Katka, she threw him a ball with the speed $v_{0}=25\;\mathrm{m}\cdot \mathrm{s}^{-1}$ and an angle of elevation $α_{0}$. In that moment, he started running towards her with the speed $v_{1}=5\;\mathrm{m}\cdot \mathrm{s}^{-1}$. Find a general formula for an angle $φ$ as a function of time, where the angle $φ(t)$ is the angle between the horizontal plane and the line between the rat and the ball. Draw this function into a graph and, based on the graph, determine, whether it's possible for the ball to obscure the Sun for the rat, when the Sun is situated $φ_{0}=50°$ above the horizon in the direction of the running rat. Use the acceleration due to gravity $g=9.81\;\mathrm{m}\cdot \mathrm{s}^{-2}$ and for simplicity imagine we are throwing the ball from a zero height.
Mirek pozoroval, co se děje v trávě.
(2 points)5. Series 29. Year - 2. multiparticular
Let's have a container that is split by imaginary plane into two disjunct parts A and B, identical in size. There are $nparticles$ in the container and each of them has a probability of 50 % to be in part A and probability 50 % to be in part B. Figure out the probabilities of the part A containing $n_{A}=0.6n$ or $n_{A}=1+n⁄2$ particles respectively.. Solve it for $n=10$ and $n=N_{A}$, where $N_{A}≈6\cdot 10^{23}$ is Avogadro's constant.
(3 points)4. Series 29. Year - 3. Save the woods
We have a toilet paper roll with the diameter $R=8\;\mathrm{cm}$ with an inside hollow tube of diameter $r=2\;\mathrm{cm}$. Every layer of the paper has the thickness $d=200µm$ and the layers lies perfectly on top of each other. By how many does the number of pieces of the paper differ had we used a piece of the length $l_{1}=9\;\mathrm{cm}$ instead of $l_{2}=13\;\mathrm{cm}?$ A part of the solution has to be an estimate of the approximation error (if you use one).
Bonus: Calculate the precise length of the spiral the toilet paper makes.
(6 points)3. Series 27. Year - S. Aplicational
- In the text of the seriesy we used the approximative relation √( 1 + $h)$, where $his$ a small value. Determine the precision of such an approximation. How much can $h$ differ from zero so that the approximated value and the precise one shall differ only by 10%? We can make a similar approximation for any „normal“ (read occuring in nature) function using Taylor's series expansion. Try to find the Tylor's series of cos$h$ and sin$h$ on the internet and neglect factors with a higher order than $h$ and find the approximate border value where it differs by approximately 0.1.
- Considering a wave equation for a classical string from the serial and let the string be fastened on one end in the point [ $x;y]=[0;0]$ a na druhém konci v bodě [ $x;y]=[l;0]$. For what values of $ω,α,aabis$ the expression
$$y(x,t)=\sin ({\alpha} x)\left [a\sin {({\omega} t)} b\cos {({\omega} t)}\right ]$$
a solution of the wave equation? Tip Subsitute into the equation for motion and use the boundary conditions.
- In the previous part of the series we were comparing different values of action for different trajectories of different particles. Now calculate the value of Nambu-Gota's action for a closed string which from time 0 to time $t$ stands still un the plane ( $x¹,x)$ and has the shape of a circle with radius $R$. Thus we have
$$X({\tau} , {\sigma} )=(c{\tau} , R\cos {{\sigma} }, R\sin {{\sigma} },0)$$
for $τ∈\langle0,2π\rangle$. Furthermore sketch the worldsheet of this string (forget about the last zero component) and how the line of a constant $τ$ and $σ$ look.
(2 points)2. Series 27. Year - 1. Twix
The chocolate bar Twix is 32 % coating. Assume that it has a shape of a cylinder with a radius of 10 mm. Neglect the coating of the base. How thick is the coating?
Bonus: Think of a better model of said bar.
Lukáše překvapil objem.
(2 points)1. Series 27. Year - 1. golden dam
How many bricks of 24-karat gold can you fit into the Orlík dam? What would be the pressure acting on a brick placed at the deepest point? The dimensions of a brick are 10 cm, 3 cm a 1 cm.
Karel wants to be rich.
(2 points)2. Series 26. Year - 1. from Prague to Brno
Assume that the Earth is a sphere and the surface distance between Dresden and Vienna is approximately $d=370$ km. How much is the distance reduced if you decide to dig a tunnel between those two cities instead of walking. Neglect the different altitudes. Compare the tunnel distance with walking distance. For simplicity, you can approximate trigonometric functions as $$ \mathrm{sin} α ≈ α - α^{3}/6 \,,\\ \mathrm{cos} α ≈ 1 - α^{2}/2 \,,\\ \mathrm{tg} α ≈ α + α^{3}/3 \,, $$ where the angle is assumed to be given in radians.
(4 points)6. Series 25. Year - 5. early class on eugenics
Aleš was procrastinating with his tablet when he realized that he is late for his class. The only way to make it on time was to run without stopping. Therefore he started running uphill with speed $v$. The road was inclined at an angle $α$. After a while (at time $T)$ he realized that he still carries a brick that he meant to leave in his tent. He is able to throw the brick only with an initial speed $w$. Determine the angle at which Aleš should throw the brick in order to hit his friend that is sitting in the same spot he was sitting. Is it possible that Aleš will not be able to do this? You should not account for any reaction time.
Karel was bored on the Internet.
(3 points)5. Series 25. Year - 3. pilgrimage of pharaohs
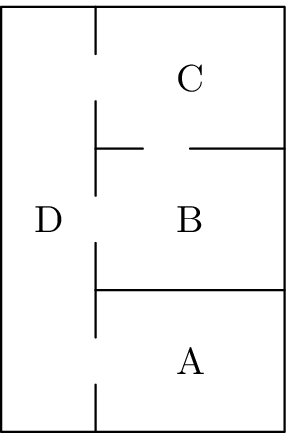
Mára decided to infect Aleš's four room apartment with pharaoh ants (top view of the apartment is on the picture). Ants are running all over the place but you can assume the following model of their motion. Every five minutes 60$%$ of ants in each room moves to the neighboring rooms and the rest stay where they are now. If there is more than one neighboring room assume that the same amount of ants moved to every one of them. This process repeats itself every five minutes (yes, assume only discrete time). The ants cannot move in or out of the apartment and they are immortal.
- If Mára places 1000 ants into the hallway (D) how many ants will be in each of the rooms after 5, 10 and 15 minutes? (2 body)
- If at some point we found out that the distribution of ants in the rooms is $N_{A}=12$, $N_{B}=25$, $N_{C}=25$ a$N_{D}=37$, how where they distributed 5 minutes earlier? (1 bod)
- *Bonus:** How would they be distributed after essentially infinite time if we start with 1000 ants in the hallway again? Does it matter how where they distributed in the beginning? And finally - will the distribution of ants in the rooms reach a stationary value or will it oscillate? (bonus points)
Karel studied Jordan form of a matrix.