Search
astrophysics (84)biophysics (18)chemistry (22)electric field (70)electric current (75)gravitational field (79)hydromechanics (144)nuclear physics (43)oscillations (55)quantum physics (31)magnetic field (42)mathematics (89)mechanics of a point mass (292)gas mechanics (87)mechanics of rigid bodies (220)molecular physics (71)geometrical optics (77)wave optics (65)other (164)relativistic physics (37)statistical physics (21)thermodynamics (150)wave mechanics (51)
mechanics of rigid bodies
(4 points)4. Series 26. Year - 5. How to build a bridge
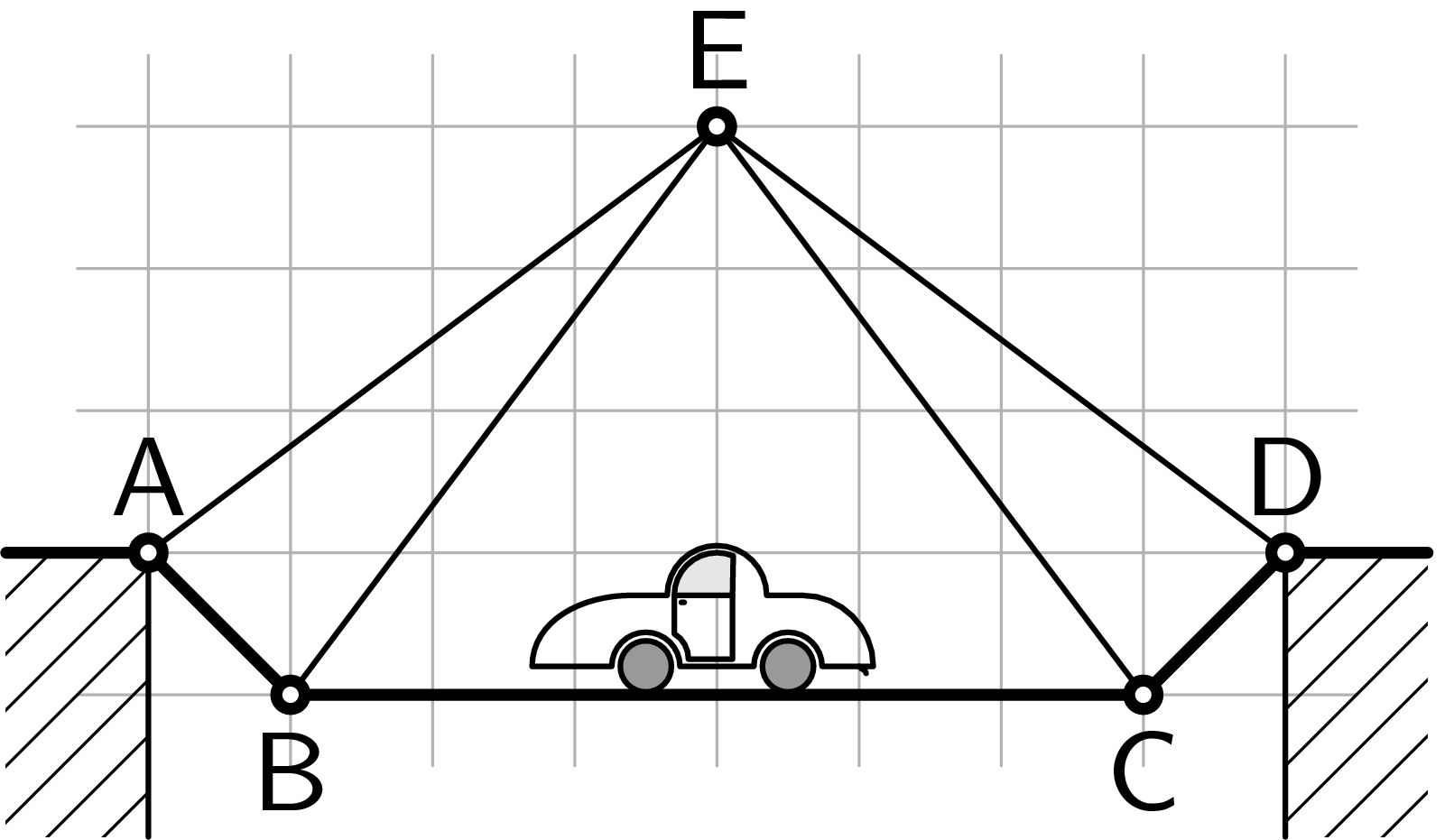
Imagine a cross section of a bridge as depicted in the picture. It consists of massless rods attached at the points $\bodA$, $\bodB$, $\bodC$, $\bodD$ and $\bodE$. Determine which rods would exhibit pressure forces and which pulling forces if a car of mass $m$ is placed on the rod $\bodBC$. You should use the picture to estimate the lengths of the rods.
Bonus: Assume that the linear density of the rods is $λ$ instead of zero.
Karel spying at a construction site.
(4 points)3. Series 26. Year - 3. Burning brakes
What is the optimal speed for a car to go downhill in order for the brakes to be warming up with the fastest rate? Assume that the temperature difference between the brakes and the air around them is directly proportional to the power dissipated in the brakes.
Lukas was on fire.
(5 points)3. Series 26. Year - 5. Gas crises
A Siberian gas pipeline with a liquefied natural gas needs to be closed. Váňa Vasilijevič decided to do this manually by closing a frictionless valve. What is the work he needed to do so? What is the force he acted on the valve with (choose an appropriate parameter to describe it)? You can imagine the valve as a board that is being inserted into the pipeline (the pipeline is perpendicular to this board). Initially, the pressure inside the pipeline was $p=2MPa$. Its cross-section is square-shaped with a side of length $a=1\;\mathrm{m}$. The board is $d=10\;\mathrm{cm}$ wide, the density of liquefied natural gas is $ρ=480\;\mathrm{kg}⁄m$, and its flow rate is $q=20m3\;\mathrm{s}$.
Ales wanted to know what is it like to live in Russia.
(8 points)3. Series 26. Year - E. Fun with cans
Determine the time dependence of the velocity of a can filled with water that is rolling down an inclined plane (starting at rest). Your inclined plane should be at least 2 meters long. Also it must be a plane! I.e. check that it is not bent, and that its surface is smooth. You can perform the measurement for example by recording the motion on a video, or by partitioning the inclined plane into several intervals and measuring the average velocity on each of them.
Karel inspired by his past.
(2 points)2. Series 26. Year - 2. hollow Earth
Imagine that all the mass of the Earth is remodeled into a spherical shell. The thickness of the shell is $d=1\;\mathrm{km}$. Assume the density remains the same, what is the outer radius of the new planet? What is the gravitational acceleration on its surface?
(4 points)2. Series 26. Year - 3. life in Venice
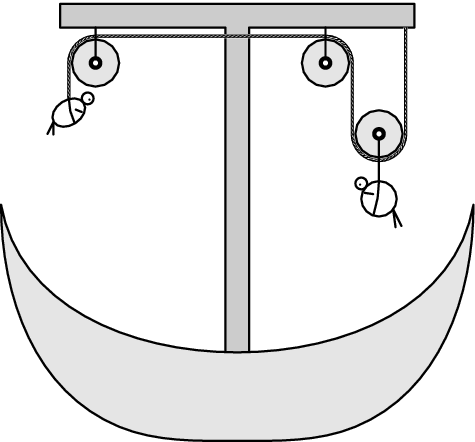
Two chubby residents of Venice Paolo and Francesca Muschetti (with masses $m_{P}=180\;\mathrm{kg}$ and $m_{F}=130\;\mathrm{kg})$ decided to go for a gondola ride. However, none of the gondoliers would allow them to enter the boat because it would sink. Fortunately, they managed to find one gondolier who designed the device shown on the picture. Both Paolo and Francesca were tied to the ends of the rope in such a way that at first Francesca was at the top but then she switched with Paolo. How tall should this device be in order for the boat to traverse the canal? The travel time is $τ=60\;\mathrm{s}$. Assume that if this device is used, the gondola does not sink. You can neglect any friction, the mass of the rope and the moments of inertia of all the pulleys.
(5 points)2. Series 26. Year - 4. a hamster
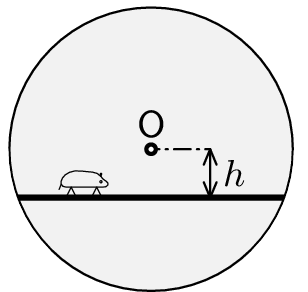
Imagine the toy for hamsters depicted in the picture. The cylinder is free to rotate around the center point $O$. The hamster stands on the horizontal plate that is glued to the cylinder at a distance $h$ from the axis of rotation. How should the hamster move in order for the plate to stay in the horizontal position? The coefficient of friction between the hamster and the plate is $f$.
(4 points)1. Series 26. Year - 4. crash tests
Two cars are driving towards each other with speed $v_{0}$. At what distance from each other should they hit the brakes in order to avoid a crash? Consider the case when both cars are on a flat road as well as the case when they are on a road inclined at an angle $α$. Both drivers apply the brakes at the same time. The braking force is equal to $f\cdot N$ where $N$ is the component of the car's weight normal to the road.
Petr played the game of chicken.
(8 points)1. Series 26. Year - E. Aleš is going bald
In this problem you are asked to investigate some elastic properties of a human hair. First you should carry out an experiment to obtain the dependence of the magnitude of the applied force on the change of the hair's length. This will allow you to construct a graph describing the dependence of the applied stress on the strain. Using these data try to estimate the maximal allowed stress and perhaps also other characteristics of the hair. You should make at least 3 measurements using hair from the same person.
Hint: The longer the hair, the better. You can measure the diameter of a hair using a micrometer or a laser in your school. Convenient weights are coins which usually have a well defined mass.
Karel was in a barber shop.
(5 points)1. Series 26. Year - P. airship
What is the minimal wind speed necessary to blow away a paper lying on a flat table?
Karel does not like wind.