Search
astrophysics (84)biophysics (18)chemistry (23)electric field (70)electric current (75)gravitational field (80)hydromechanics (145)nuclear physics (44)oscillations (56)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (295)gas mechanics (87)mechanics of rigid bodies (220)molecular physics (71)geometrical optics (77)wave optics (65)other (164)relativistic physics (37)statistical physics (21)thermodynamics (151)wave mechanics (51)
relativistic physics
5. Series 21. Year - 4. Sun can
Rama travels between the stars in such way, that one half of time is constantly accelerating and second half of time is slowing down. Currently the Rama is on parabolic trajectory around the Sun with peak on Earth orbit. It gets energy from Sun light. Its surface absorbs 80 % of incident energy. Will it get enough energy to get to Sirius, which is in distance of 12 light years in less than 24 years?
Nadhodil Jakub Benda
2. Series 21. Year - 4. charged aerial
Two identical charges are at the end of stiff non-conductive rod. What power will be needed to rotate rod at constant angular speed with axis going through the middle of the rod? The friction is negligible
Úlohu vymyslel Martin Výška.
3. Series 19. Year - 2. raid at a lens
Lets have a lens of focal length $f$. The light source is at optical axis in distance $a>f$ from the lens. The light source starts moving at constant speed towards the lens. Calculate the speed of movement of the image of the light source. Decide, if this speed can be bigger than the speed of light. Would it contradict special theory of relativity?
Vymyslel Jarda Trnka, když psal studijní text z optiky.
6. Series 18. Year - 2. how to make a black hole
When the star is compressed (or any other body) into a sphere of radius $r_{g}$, the black hole is created. So called Schwarzschild's radius $r_{g}$ can be interpreted in classical physics as a radius of a body of mass $M$, where the exit velocity is equal to the speed of light $c)$.
Knowing the mass of the star $M$ calculate Schwarzschild radius $r_{g}$ and critical density of the star $ρ$, at which it collapses into black hole. Solve for arbitrary values and then for the masses of Earth, Sun and the galaxy nucleus 100 billions heavier than Sun.
Jarda
6. Series 18. Year - E. catch a photon
Measure the speed of light in vacuum. Use any method, for example use microwave oven.
Co jiného dát jak exp do roku fyziky.
6. Series 18. Year - P. trip to Stonehenge
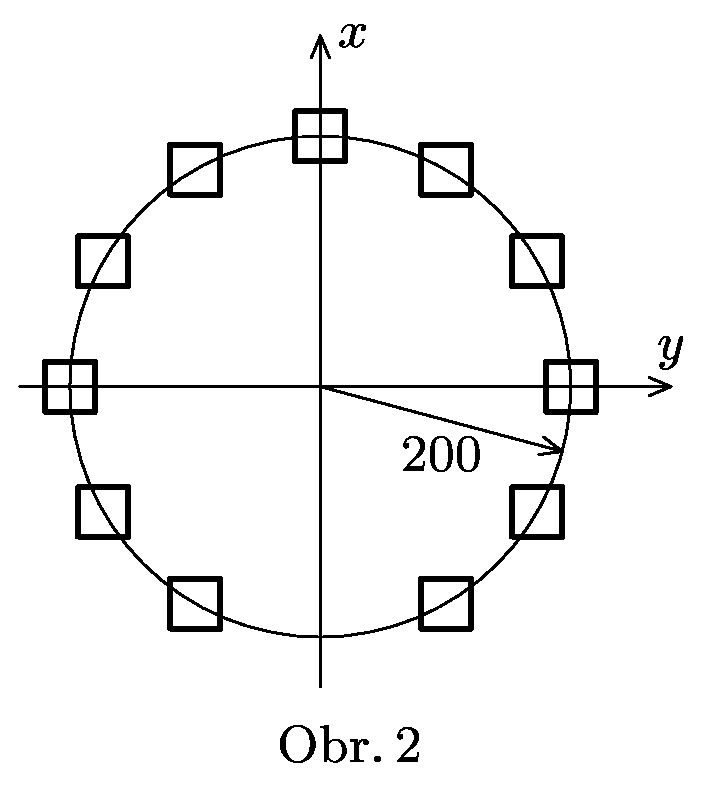
Imagine a trip in a rocket over Stonehenge. The Stonehenge is made from stone blocks in the the shape of regular dodecagon (object with 12 corners – see figure 2) of radius 200. You fly above the axis $x$ at the height $z=50$ and are looking in horizontal direction. When you are in the point of coordinates ( $-200$, $0)$ and ( 0$$, $0)$ you see the world exactly as in the image 6 respectively, while both of you have same eyes (at least the view angle:-). Calculate (approximately) the ratio of the speed of the rocket and the speed of light from the images.
Matous.
4. Series 18. Year - 3. limousine in the shed
One of the winners of Superstar (equivalent of 'You are a star'/'Eurovision song contest') has suddenly a problem. His new limousine is too long to fit in his old shed. His friend, student of physics and lover of Albert Einstein work, suggested that if the limousine drives fast it contracts in the frame of stationary observer. And if the speed is large enough, it will fit into the shed.
At the beginning and the end of shed are trap doors which fall when the limousine is all inside. But from the point of view of driver the in the limousine, due to the length contraction the shed is shorter and the limousine cannot fit in!
Decide, if is possible to park the limousine in the shed.
Podle úlohy z přednášky z STR.