Search

• Some stars are considered circumpolar. Does it mean that they can be seen the whole year? What stars are visible throughout the whole year in Czech Republic? What coordinate describes circumpolar stars? What is the situation in Czech Republic, at the pole and at the equator? We recommend that you download the program <a href=http://www.stellarium.org/>Stellarium</a> (GNU GPL license) where you can enter your location and look at these different cases.

• Compare the absolute magnitudes of Alpha Lyrae (7.79 pc far, apparent magnitude 0.01 mag) and Betelgeuze (Alpha Ori, approximately 200 pc far, apparent magnitude 0.42 mag). How would we see these stars if they exchanged their distances from the Earth? Discuss visibilities.

• Transformations and some more transformations. Find the transformation between galactic and equatorial coordinates or the second kind. Do not worry if the resulting equations do not look exactly like those found in literature.

• Janap likes to get lost once in a while. It is not always desired but it happens anyway. This time however she brought a theodolite – a magic box that can measure how high above a horizon a star is. She found out that the star Arcturus was located at 23.20 gon at 18:46:30 and the star Capella at 13.60 gon at 19:18:30. The scale of theodolite was in grad (gon), where 100 gon = 90°. What was her location?

How would the power of sunlight hitting the Earth in aphelion change if we were to accelerate the Earth in the direction of motion in such a way to extend a year by a week? Estimate the temperature of the Earth in aphelion and perihelion if its heat capacity is almost zero. For simplicity assume that the original trajectory of the Earth was circular (not the case after the velocity boost).

Sometimes the Moon can look like a little ship. What are the conditions (time and place) for this to happen? If you get stuck with this problem you can consult a software like Celestia.

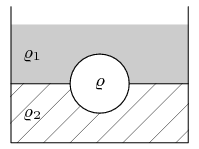
A solid sphere of density ρ is placed between two layers of immiscible liquids (see picture). Densities of the upper and lower liquids are ρ_{1} and ρ_{2} respectively. Assume that ρ_{1} ρ < ρ_{2}. Calculate the fraction of the sphere surrounded by the upper resp. lower liquid.

The year 2009 is international year of astronomy and remembers 400 years from discovering telescope. Lets go back 400 years to the times, when the telescope was already invented, but the classical physics was just in its beginnings. At this time there were two explanation of world: Copernicus's heliocentric and Ptolemaios's geocentric. Design an experiment, which will be able to decide which of above models is correct. Document, what results you can expect and how you can interpret it. You do not have to make the observation itself. Explain, why in geocentric model the Sun and Earth are connected by a line.

Rama travels between the stars in such way, that one half of time is constantly accelerating and second half of time is slowing down. Currently the Rama is on parabolic trajectory around the Sun with peak on Earth orbit. It gets energy from Sun light. Its surface absorbs 80 % of incident energy. Will it get enough energy to get to Sirius, which is in distance of 12 light years in less than 24 years?

• Derive Taylor expansion of exponential and for $x=1$ graphically show sequence of partial sums of series \sum_{$k=1}^{∞}1⁄k!$ with series { ( 1 − 1 ⁄ $n)^{n}}_{n=1,2,\ldots}$.

Using the same method compare series { ( 1 − 1 ⁄ $n)^{n}}_{n=1,2,\ldots}$ and series of partial sums of series \sum_{$k=1}^{∞}x^{k}⁄k!$, therefore series {\sum_{$k=1}^{n}x^{k}⁄k!}_{n=1,2,\ldots}$, now for $x=-1$.

• The second task is to find concentration of electrons and positrons on temperature with total charge $Q=0$ in empty and closed cavity (you can choose value of $Q.)$ Further calculate dependence of ration of internal energy $U_{e}$ of electrons and positrons to the total internal energy of the system $U$ (e.g. the sum of energy of electromagnetic radiation and particles) on temperature and find value of temperature related to some prominent temperature and ratios (e.g. 3 ⁄ 4, 1 ⁄ 2, 1 ⁄ 4, …; can this ratio be of all values?).

Put your results into a graph – you can try also in 3-dimensions.

To get the calculation simplified, it could help to take some unit-less entity (e.g. $βE_{0}$ instead of $β$ etc.).

• Solve the system of differential equations for $M(r)$ and $ρ(r)$ in model of white dwarf for several well chosen values of $ρ(0)$ and for every value find the value which it get close $M(r)$ at

$r→∞$. This is probably equal to the mass of the whole star. Try to find the dependence of total weight on $ρ(0)$ and find its upper limit. Compare the result with the upper limit of mass for white dwarf (you will find it in literature or internet). Assume, that the star consists from helium.

Find the properties of material, which you need to make a rope for a lift from geostationary orbit to the Earth surface. Is such material available on Earth?