Search
astrophysics (85)biophysics (18)chemistry (23)electric field (70)electric current (75)gravitational field (80)hydromechanics (146)nuclear physics (44)oscillations (56)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (295)gas mechanics (87)mechanics of rigid bodies (220)molecular physics (71)geometrical optics (77)wave optics (65)other (164)relativistic physics (37)statistical physics (21)thermodynamics (153)wave mechanics (51)
electric field
(8 points)4. Series 26. Year - E. Fun with straws
You can charge a regular plastic straw by rubbing it with a piece of fabric. This charge can be so large that the straw might even attach itself to a wall or a whiteboard. Explain this phenomena and estimate the charge you can put on a single straw.
Hint: You might need to use two straws.
Karel ran out of drawing pins.
(6 points)3. Series 26. Year - S. tokamak
- Calculate the specific resistance of hydrogen plasma at temperature 1 keV. Compare your result with the resistance of common conductors.
- Calculate the current necessary to create a sufficiently strong poloidal magnetic field in a tokamak with a major radius of 0.5 m. The toroidal field is created using a toroidal coil with 20 windings per meter. The current inside this coil is 40 kA. The magnitude of the poloidal field should be approximately 1/10 of the magnitude of the toroidal field.
- Create a physical model of the field lines of the force field inside the tokamak, take a photo of it, and send it to us.
(2 points)5. Series 25. Year - 2. electric equilibrium
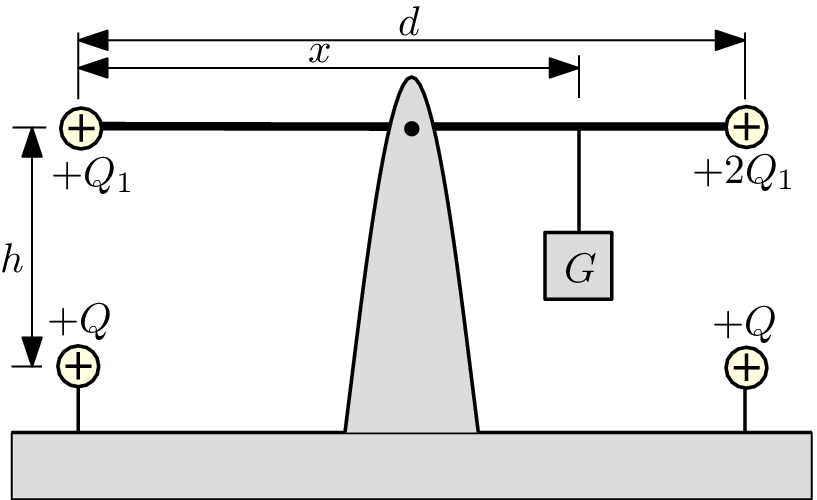
An insulating rod of length $d$ and negligible mass can rotate around its middle point (see picture). There are small balls of negligible mass and charges $Q_{1}$ and 2$Q_{1}$ on both of its ends. Due to the weight $G$ (see picture) the system is in mechanical equilibrium. Distance $h$ under each of the small balls is a another ball with charge $Q$.
- What is the distance $x$ for which the rod is horizontal and is in equilibrium?
- What is the distance $h$ such that the rod is in equilibrium but there is no force on the pivot that holds it?
Dominika dug into old problem sets.
(5 points)3. Series 25. Year - 5. gas leakage
Imagine two infinitely large grounded conducting planes distance $l$ apart. There is a charge placed between them and distance $x$ from one of them. What is the induced charge on the other plane?
Aleše napadlo při úniku.
(4 points)1. Series 25. Year - 4. drrrrr
A small conductive ball of negligible size is bouncing between two charged plates of opposite polarities. What is the frequency of the resulting periodic motion of the ball? Voltage between the plates is $U$. When the ball touches a charged plate it charges to a charge of magnitude $Q$ whose polarity is the same as polarity of the plate. The ratio of kinetic energies of the ball before and after an impact is $k$.
Bonus: Does the output power of this resistor correspond to the energy losses during impacts?
Jáchym
5. Series 24. Year - P. chordates
As you know the amount of positive charges in the Universe is the same as the amount of negative charges. An argument for this statement is that if it were not so the repulsive electric force would be greater than the attractive gravitational force and objects would not hold together. However is this equilibrium perfect? What if there are more positive charges than negative ones and the electric force just reduces the gravitational attraction? Describe an experiment that would enable us to find out any discrepancy from this equilibrium. What is the minimum discrepancy we would be able to measure with such an experiment? As a measure of this discrepancy you can take the ratio of total charge/(positive charge-negative charge) in some large volume.
6. Series 22. Year - 2. escape from the charged sphere
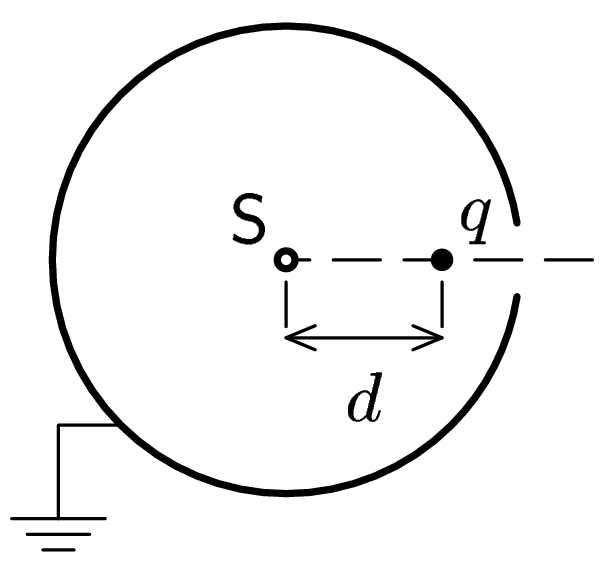
Inside of grounded conductive sphere is made a small orifice, just big enough for a small charged particle to pass through. Assume the particle is placed in distance $d$ from the center of the sphere (see picture).
The charged particle is set free. How far it will fly off from the sphere? Try to use method of mirror potential.
nad koulemi rozjímal Pavel M.
5. Series 22. Year - S. games with electrons
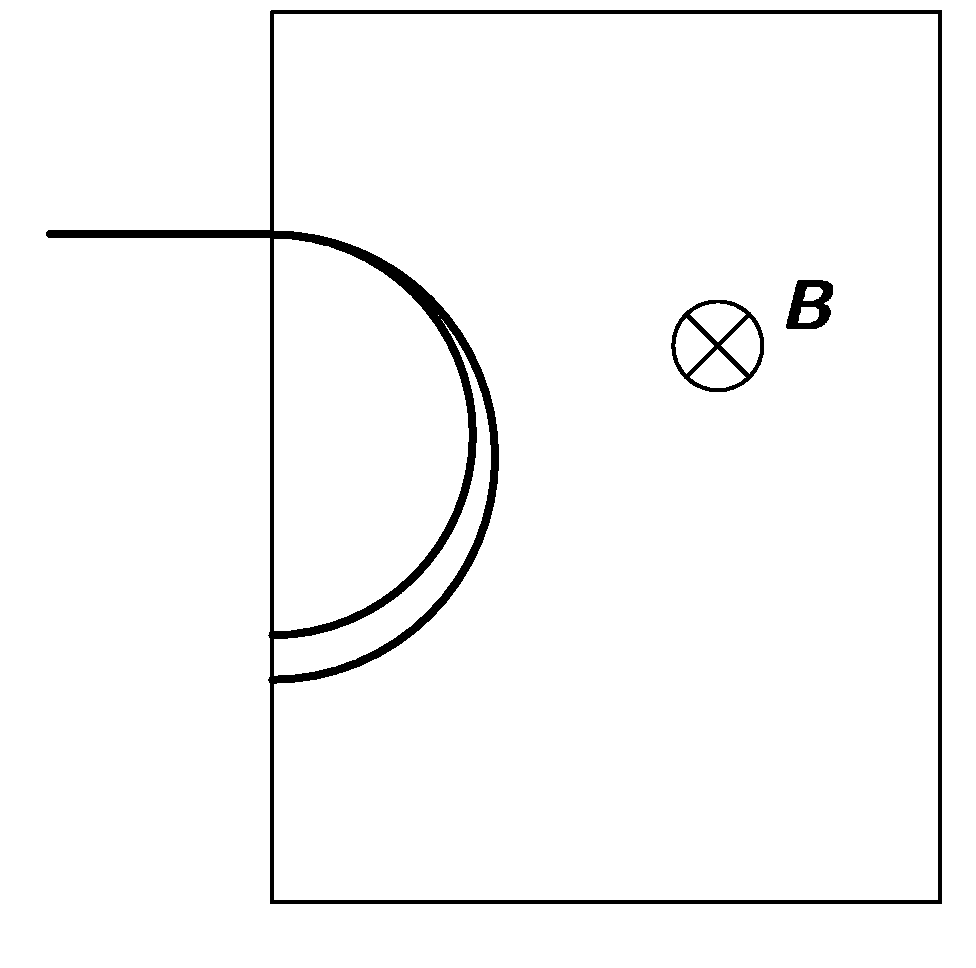
- The second method to measure specific electron charge used by J. J. Thomson is observation of deflection of cathode ray by electric field. Assume apparatus as on the figure. How depends deflection of the beam observed on the screen on the right on the electrical voltage, speed and geometrical dimensions of apparatus?
- The one of problems which was J. J. Thomson facing during measurement of specific electron charge was following: After the beam entered magnetic field, the beam has spread into a bigger area (see figure). The dispersion is causing some error in measuring position of electrons (Thomson mentioned up to 20%). How can be this dispersion explained? How can be this inaccuracy improved (this is for bonus point)?
- By using the data from table calculate charge of electron in case, that the oil had density of 920 kg\cdot m^{ − 3}, air density was 1,2 kg\cdot m^{ − 3} and viscosity 17,1 \cdot 10^{−7} Pa\cdot s. Used electric field was 250 kV\cdot m^{ − 1}.
Zadali Pavel M. a Jakub B.
3. Series 21. Year - 4. particle in field
Assume constant electrostatic field in time. Lets insert a charged particle into the field with zero speed. When we record the trajectory of particle, we see that it does not depend on its mass. Can you explain it?
Na problém narazil Marek Scholz při programování zápočťáku.