Search
astrophysics (85)biophysics (18)chemistry (23)electric field (70)electric current (75)gravitational field (80)hydromechanics (146)nuclear physics (44)oscillations (56)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (295)gas mechanics (87)mechanics of rigid bodies (220)molecular physics (71)geometrical optics (77)wave optics (65)other (164)relativistic physics (37)statistical physics (21)thermodynamics (153)wave mechanics (51)
hydromechanics
1. Series 23. Year - 4. emptying centrifuge
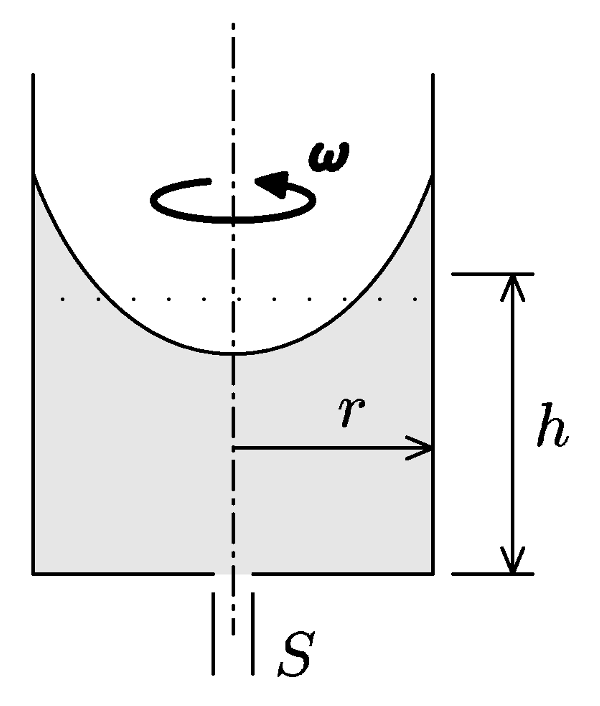
Lets have a tall cylindrical vessel filled with water (radius $r$, height of water $h)$ and spin it around its axis at angular speed $ω$. At the centre of bottom is a small orifice of surface area $S$, while the vessel is still rotating. How much water will escape the vessel?
Archivní víno.
5. Series 22. Year - 3. the Earth
What was the speed of Earth rotation during solidifying of Earth to have the difference between Equator radius and pole radius same as today?
na schůzku donesl Honza Jelínek
5. Series 22. Year - E. WC
Measure, how high the water will splash during fall of different bodies onto a water level. Observe the dependence of height, shape and mass of falling object. What percentage of energy is used to create waves on the water level?
na oné místnosti vymyslel Jakub Benda
4. Series 22. Year - S. Foucault pendulum and Earth rotation
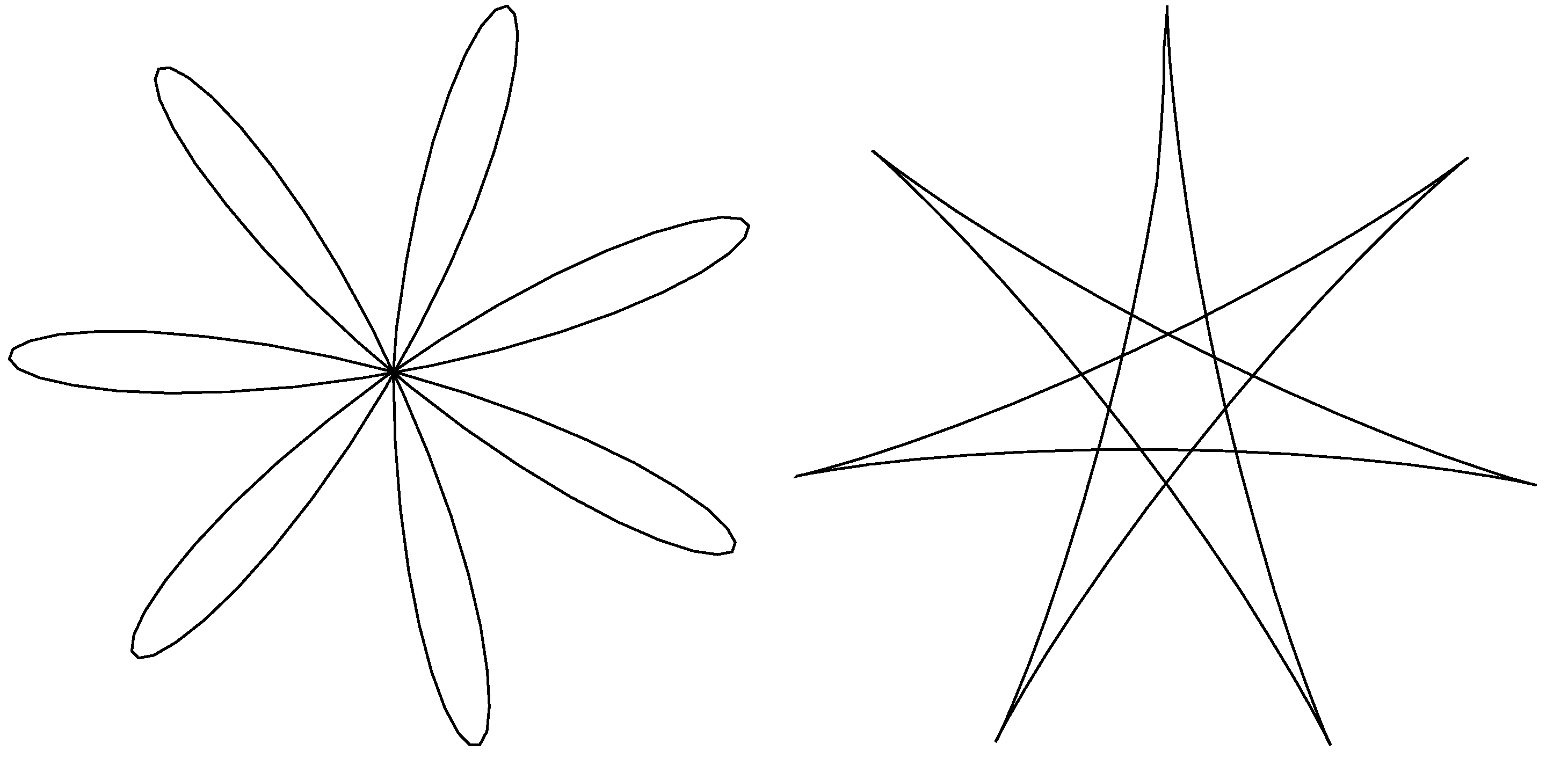
- Foucault pendulum has drawn into a sand at two different demonstrations two different diagrams, as on the picture. Find out, what caused different shape and how long the pendulum was to create such diagrams on the floor of Paris cathedral. How many tips do the stars have in reality?
- What shape will have the water level in barrel standing still at horizontal plane?
- Show, that equation
$$δf=f_{+}-f_{-}=4**ω**\cdot \textbf{S}/(λ_{0}P)$$ for frequency difference (frequency of beats) of two contra-propagating light beams in laser gyroscope, is valid for any shape of gyroscope, not only circle.
K procvičení probrané látky zadali autoři seriálu.
3. Series 22. Year - 1. hydrogen
Fykos organisers were left with a container with compressed hydrogen. And they plan to transfer all hydrogen into a light balloon (so it will have atmospheric pressure). Is such balloon able to lift the container, if the temperature is constant?
Z maďarské přípravy na FO od Dalimila vybral Aleš.
3. Series 22. Year - E. in vino veritas
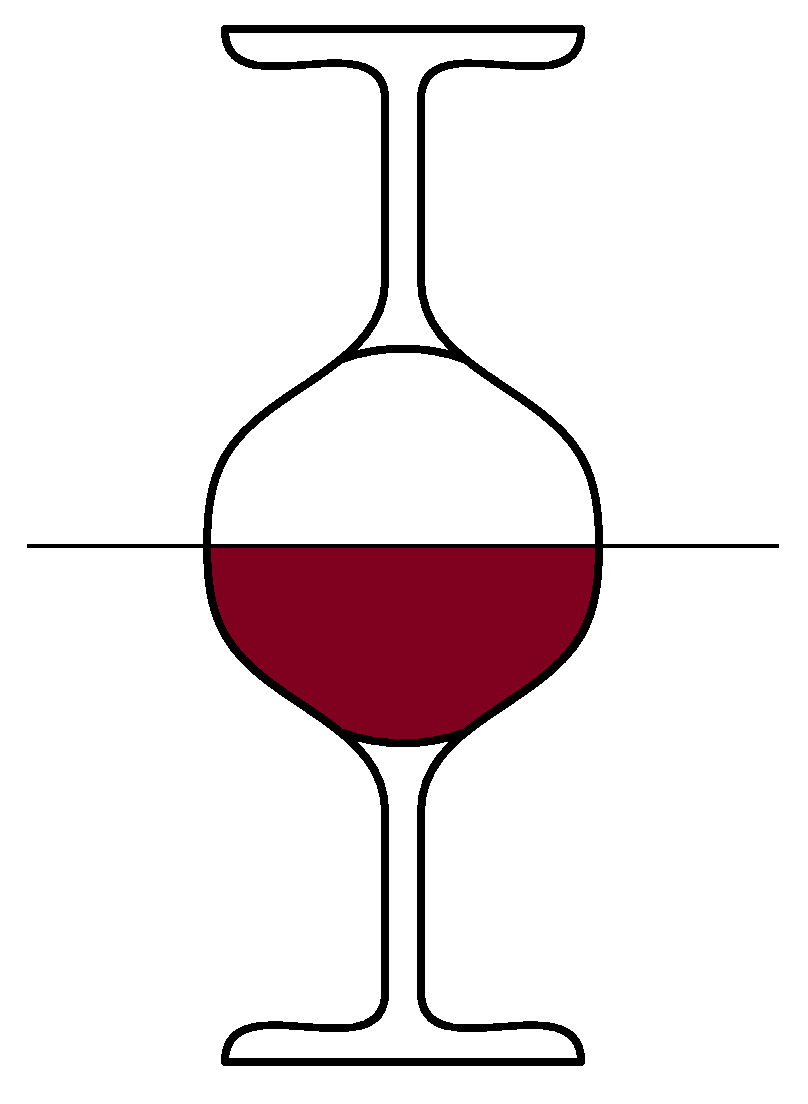
Try following experiment: Fill the same glasses one with water, second with wine up to the top. Put a sheet of paper on the glass with water. Then turn the glass with water upside down and face it with the glass with wine (final state is on the figure). Now try to remove the paper and you will see very strange effect: the content of glasses will change, without mixing (it takes a time, be patient). Find out, why it is as it is. How is the time for change dependent on surface area, alcohol concentration and other parameters? Will this happen also for other liquids? E.g. coloured water, milk, oil…
Na přednášce na vlastní oči viděl Jakub M.
6. Series 21. Year - 3. cooling a soup
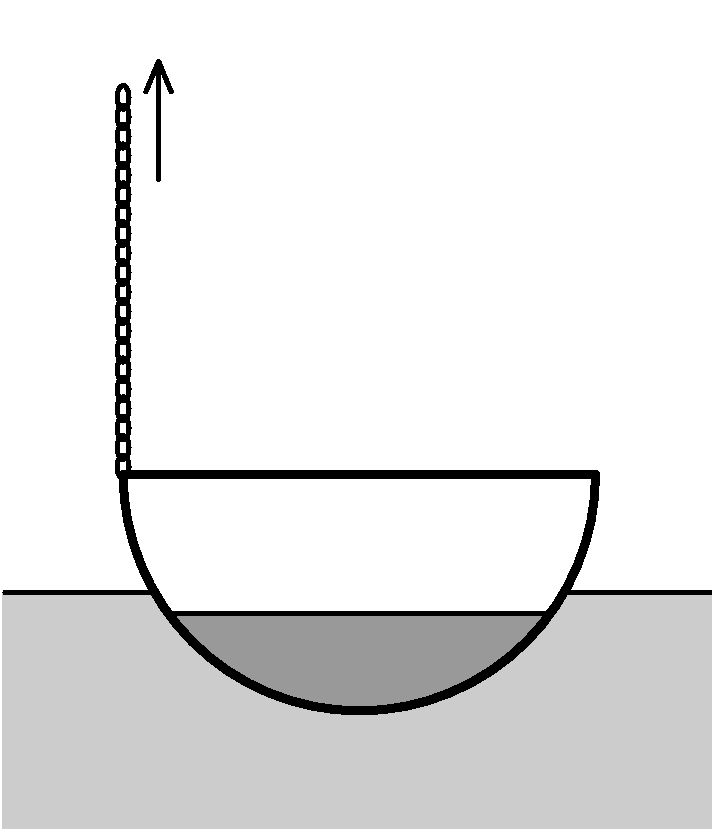
Assume copper hemispherical pot, with diameter of 40 cm. The pot is filled with a soup and is placed in water. It is floating 10cm under water level. Will the water start to fill the pot, if the border of pot is pulled up by a chain by 10 cm?
Sbírka od Dalimila Mazáče.
3. Series 21. Year - P. high and low tide
High tide and low tide are caused by tidal forces, mainly gravitational force of the Moon. High tide repeats every 12 hours and 25 minutes, however on the Earth we always see two high tides on opposite sides of the Earth. It means that one high tide circles the Earth in approximately twice the time which is 25 hours. Therefore on the equator of length 40 000 km the high tide is moving at speed approximately 40 000/25 km ⁄ h = 1 600 km ⁄ h. This is even more that the speed of sound in air.
However, from the experience we know, that water in ocean does not move at this speed, at the ships does not shipwreck regularly and bring bananas from Kostarika. Is there some mistake in calculation, or do we have to interpret it differently?
Úlohu navrhl Honza Hradil.
2. Series 21. Year - 3. wine is flowing
Wine makers and truck drivers know how to move liquid from heavy containers. Winemaker Ignac wants to move wine from one container to another. First he puts empty container on the ground and full to the level $Δ$. Then both containers are connected by a tube and with help of little suction wine starts to flow to bottom container. How long it will take? Assume, that both containers are same cylinders of radius $R$ and height $H$.
Vymyslel Jano Lalinský.
2. Series 21. Year - E. bubo bubo
Verify experimentally following hypothesis: the rotation of Earth causes water on north hemisphere to swirl to right, on south hemisphere to left. For your conclusion to have relevance, enough number of measurements must be done at different conditions.
Napadlo zadat Honzu Prachaře.