Search
astrophysics (85)biophysics (18)chemistry (23)electric field (71)electric current (75)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (71)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (154)wave mechanics (51)
mathematics
(5 points)5. Series 25. Year - 4. mother and a stroller
Mother is connected to a stroller of mass $m$ with a string of length $l$ that is initially fully stretched. The coefficient of friction between the floor and mother resp. stroller is $f$. Mother starts pulling the stroller with constant velocity $v$ that is perpendicular to the initial orientation of the string. Describe the dependence of the trajectory of the stroller on system parameters. Assume both the mother and the stroller have negligible size. We recommend that you numerically simulate this problem.
final exam
(3 points)4. Series 25. Year - 3. flying stone
How long will it take for a spherical stone of mass $m$ to reach the bottom of a pond $d$ meters deep if you throw it in from height $h?$ How will the answer change if the stone is „flat“ and not spherical?
Dominika házela šutry.
(4 points)4. Series 25. Year - 4. rockets
Model of a rocket contains a motor whose power output is constant as long as it is provided with fuel. The initial mass of the fuel is $m_{p}$, the mass of an empty rocket is $m_{0}$ and the amount of fuel burned by the motor grows linearly with time. What is the maximum height the rocket can reach assuming the gravitational field to be homogeneous and the air resistance to be negligible?
Michal odpaloval rakety.
(2 points)1. Series 25. Year - 1. light bulb
Pepička has bought a light bulb, two switches and a wire. Help: her to design a circuit such that if you change the state of any of the switches the light bulb will also change its state (from on to off or reverse). After you find the solution try to generalize it to any number of switches.
Marek S.
(2 points)1. Series 25. Year - 2. struggling swimmer
A man wants to swim across a river which flows at a speed of 2 km/h. He is able to swim at a speed of 1 km/h. What is the optimal trajectory and direction he should take so that his trip is the least exhausting? Where and at what time will he reach the other bank? How would the situation change if his aim was the shortest possible trajectory? The width of the river is $d=10\;\mathrm{m}$.
Petr
5. Series 24. Year - S. aviation
- How would you draw (using only drawing-compass and a ruler) the Zhukovsky profil?
- Draw the streamlines around the Zhukovsky profile. Choose the parameters $d/l$ and $m/l$ so that they have real world justification.
- What is the lifting force acting on a square board? On a semicircular board?
- Draw the profile of a wing that corresponds to the Kármán–Trefftz transform.
Jakub
1. Series 24. Year - S. complex warm-up
- Convince yourselves that the nth roots of a complex number of modulus one lie on a regular $n-gon$ and solve the Bombelli equation $x^{3}-15x-4$ = 0. (see the text for hints)
- Express the identities concerning sin(α+β) and cos(α+β) using the complex exponential.
- Show that we were allowed to neglect the higher powers in deriving the Bernoulli limit, i.e. show that it was legitimate to add the o(1/$N)$ term inside the parentheses.
- Use the little-o notation to solve the problem of small oscillations around equilibrium point in Yukawa potential $V$ = $k \exp(x/λ) /$ $x$.
- Prove that the Chebyshev polynomials cos($n$ arccos $x)$ are really polynomials.
Hint: Let's have a unit complex number $z$ with real part $x$. Then, the expression is equal to the real part of $z^{n}$.
Jakub Michálek a Lukáš Ledvina
5. Series 22. Year - 1. turning a carpet
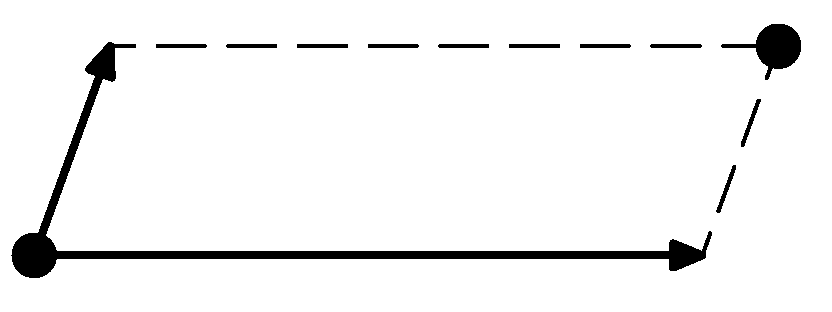
Choosing two different vectors in a plane and shifting the origin, an infinite grid of nodes can be created (see picture). Using the same approach in 3D will make a crystal lattice. If such grid is shifted by one of the vectors, we will get identical grid. Also rotation of the grid by some angle will generate identical grid. Find out all angles which can be basis for rotationaly symetrical grid and draw how such grid looks like.
Zadal Honza Prachař, základní otázka krystalografie.
1. Series 22. Year - 3. do not cradle me
Kathy is on a swing (a plank suspended on 2 ropes). At high displacements she kneels down, in lowest point she gets up. This movements she periodically repeats. Ration of distance of centre of gravity from the rotation axis at kneeling down and at standing is 2^{1 ⁄ 12} ≈ 1,06. How many times Kathy must swing to double the amplitude of swinging?
Z asijské olympiády přinesl Honza Prachař