Search
astrophysics (85)biophysics (18)chemistry (23)electric field (71)electric current (75)gravitational field (81)hydromechanics (146)nuclear physics (44)oscillations (57)quantum physics (31)magnetic field (43)mathematics (89)mechanics of a point mass (298)gas mechanics (87)mechanics of rigid bodies (221)molecular physics (71)geometrical optics (78)wave optics (65)other (167)relativistic physics (37)statistical physics (21)thermodynamics (154)wave mechanics (51)
mechanics of a point mass
(4 points)6. Series 25. Year - 3. a pump
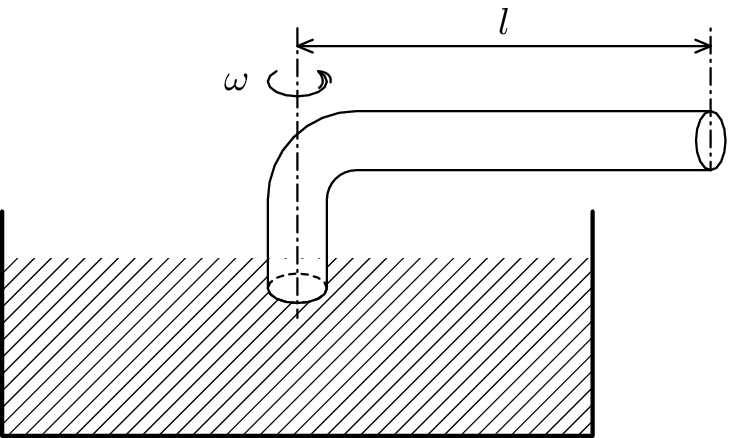
Imagine a bent tube of length $l$ that is full of water and whose lower end is submerged in a container (see \ref {S6U3_trubice}). We rotate the tube once per time $T$. Calculate the pressure that causes the water to flow out of the container. You can neglect viscosity and the pressure due to the column of water in the vertical part of the tube.
Exhausted Petr.
(4 points)6. Series 25. Year - 5. early class on eugenics
Aleš was procrastinating with his tablet when he realized that he is late for his class. The only way to make it on time was to run without stopping. Therefore he started running uphill with speed $v$. The road was inclined at an angle $α$. After a while (at time $T)$ he realized that he still carries a brick that he meant to leave in his tent. He is able to throw the brick only with an initial speed $w$. Determine the angle at which Aleš should throw the brick in order to hit his friend that is sitting in the same spot he was sitting. Is it possible that Aleš will not be able to do this? You should not account for any reaction time.
Karel was bored on the Internet.
(2 points)5. Series 25. Year - 1. the flu pill
Some pills against flu dissolve in water making it to fizz. At first the pill is on the bottom of the glass but after a while it rises to the surface. Why?
Lukáš wanted to avoid the flu.
(2 points)5. Series 25. Year - 2. electric equilibrium
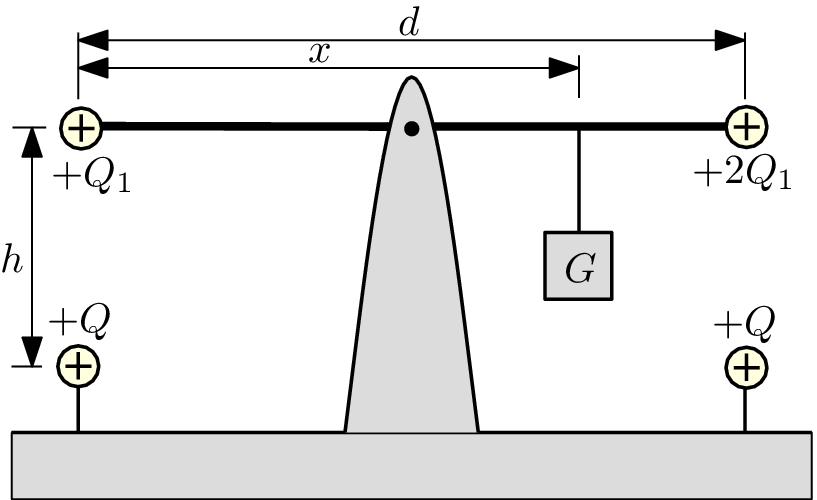
An insulating rod of length $d$ and negligible mass can rotate around its middle point (see picture). There are small balls of negligible mass and charges $Q_{1}$ and 2$Q_{1}$ on both of its ends. Due to the weight $G$ (see picture) the system is in mechanical equilibrium. Distance $h$ under each of the small balls is a another ball with charge $Q$.
- What is the distance $x$ for which the rod is horizontal and is in equilibrium?
- What is the distance $h$ such that the rod is in equilibrium but there is no force on the pivot that holds it?
Dominika dug into old problem sets.
(5 points)5. Series 25. Year - 4. mother and a stroller
Mother is connected to a stroller of mass $m$ with a string of length $l$ that is initially fully stretched. The coefficient of friction between the floor and mother resp. stroller is $f$. Mother starts pulling the stroller with constant velocity $v$ that is perpendicular to the initial orientation of the string. Describe the dependence of the trajectory of the stroller on system parameters. Assume both the mother and the stroller have negligible size. We recommend that you numerically simulate this problem.
final exam
(4 points)5. Series 25. Year - 5. hunter v2
How much should we increase the power output of train's motor per one caught bird per second if we catch the birds in a net placed on top of the car? Train moves with speed $v$, bird's mass is $m$, his speed $w$, the angle with which the bird hits the net is $φ$ and the net has area $S$. Assume that after each catch the net returns to its initial shape.
Organizers took the train.
(2 points)4. Series 25. Year - 1. stairs from Chrudim
Escalators at the subway station Náměstí Míru consist of $n$ steps and move with speed $v$. How many times do you actually have to step before you reach the end if you move a) in the same direction as the escalator, b) opposite to the direction the escalator moves. Assume that you move with speed $v_{1}$ such that $v_{1}>v$.
Aleš po cestě do otevřených dveří.
(2 points)4. Series 25. Year - 2. Gatling gun
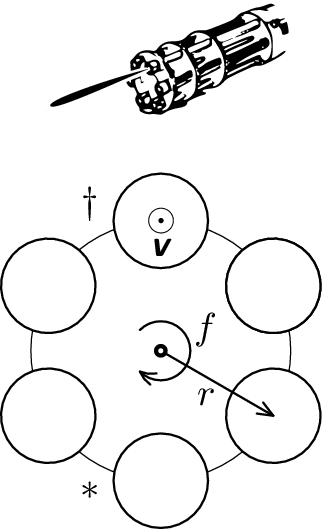
At first developed as an equipment that would simplify the distribution of seeds, gatling gun turned out to be much more useful for distributing bullets. Relative to the gatling gun's barrel, what is the region where you are in danger of being shot? The calibre is $d$, number of barrels $n$, distance from the barrel's axis to the axis of the shaft is $r$, the gun can make $f$ rotations per second, firing rate is $F$ and a bullet leaves the barrel with speed $v$.
Napadlo Michala při čtení tajného časopisu.
(3 points)4. Series 25. Year - 3. flying stone
How long will it take for a spherical stone of mass $m$ to reach the bottom of a pond $d$ meters deep if you throw it in from height $h?$ How will the answer change if the stone is „flat“ and not spherical?
Dominika házela šutry.
(4 points)4. Series 25. Year - 4. rockets
Model of a rocket contains a motor whose power output is constant as long as it is provided with fuel. The initial mass of the fuel is $m_{p}$, the mass of an empty rocket is $m_{0}$ and the amount of fuel burned by the motor grows linearly with time. What is the maximum height the rocket can reach assuming the gravitational field to be homogeneous and the air resistance to be negligible?
Michal odpaloval rakety.