Search

Imagine a bomb that is free-falling on a military base of your enemies. Although you threw the bomb off an airplane, you should assume that its motion is vertical (i.e. no horizontal component of its velocity relative to the surface). Because of air friction, the falling bomb emits a sound that propagates at the speed c = 340 m/s. What is the maximal impact velocity of the bomb in order for your enemies to hear it before it kills them?

Assume that the Earth is a sphere and the surface distance between Dresden and Vienna is approximately $d=370$ km. How much is the distance reduced if you decide to dig a tunnel between those two cities instead of walking. Neglect the different altitudes. Compare the tunnel distance with walking distance. For simplicity, you can approximate trigonometric functions as $$ \mathrm{sin} α ≈ α - α^{3}/6 \,,\\ \mathrm{cos} α ≈ 1 - α^{2}/2 \,,\\ \mathrm{tg} α ≈ α + α^{3}/3 \,, $$ where the angle is assumed to be given in radians.

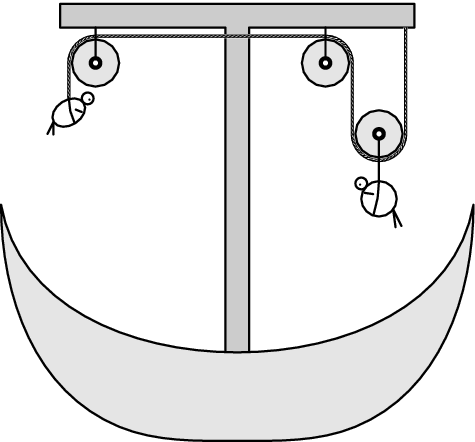
Two chubby residents of Venice Paolo and Francesca Muschetti (with masses $m_{P}=180\;\mathrm{kg}$ and $m_{F}=130\;\mathrm{kg})$ decided to go for a gondola ride. However, none of the gondoliers would allow them to enter the boat because it would sink. Fortunately, they managed to find one gondolier who designed the device shown on the picture. Both Paolo and Francesca were tied to the ends of the rope in such a way that at first Francesca was at the top but then she switched with Paolo. How tall should this device be in order for the boat to traverse the canal? The travel time is $τ=60\;\mathrm{s}$. Assume that if this device is used, the gondola does not sink. You can neglect any friction, the mass of the rope and the moments of inertia of all the pulleys.

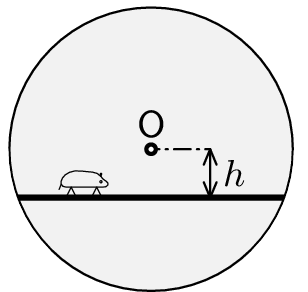
Imagine the toy for hamsters depicted in the picture. The cylinder is free to rotate around the center point $O$. The hamster stands on the horizontal plate that is glued to the cylinder at a distance $h$ from the axis of rotation. How should the hamster move in order for the plate to stay in the horizontal position? The coefficient of friction between the hamster and the plate is $f$.

Two cars are driving towards each other with speed $v_{0}$. At what distance from each other should they hit the brakes in order to avoid a crash? Consider the case when both cars are on a flat road as well as the case when they are on a road inclined at an angle $α$. Both drivers apply the brakes at the same time. The braking force is equal to $f\cdot N$ where $N$ is the component of the car's weight normal to the road.

A small ball of radius $r$ is placed on top of a bigger ball of radius $R$. The lowest point of the bigger ball is at height $h$ above ground. Both balls are released simultaneously. Calculate the maximum height that can be achieved by the smaller ball. Assume that all collisions are perfectly elastic and that the mass of the smaller ball is negligible compared to the larger ball.

Bonus: Generalize the problem if there are $N$ balls present. You can still assume that a smaller ball on top of a bigger ball has a negligible mass compared to the larger one.

Estimate the minimal energy needed to put a space station on an orbit around the Earth. You can work with the values valid for the International Space Station which orbits the Earth at height approximately $h=350\;\mathrm{km}$ and has mass $m=450000\;\mathrm{kg}$. Explain why is this estimate minimal and why, in reality, much more energy is needed.

Imagine a bent tube of length $l$ that is full of water and whose lower end is submerged in a container (see \ref {S6U3_trubice}). We rotate the tube once per time $T$. Calculate the pressure that causes the water to flow out of the container. You can neglect viscosity and the pressure due to the column of water in the vertical part of the tube.

Aleš was procrastinating with his tablet when he realized that he is late for his class. The only way to make it on time was to run without stopping. Therefore he started running uphill with speed $v$. The road was inclined at an angle $α$. After a while (at time $T)$ he realized that he still carries a brick that he meant to leave in his tent. He is able to throw the brick only with an initial speed $w$. Determine the angle at which Aleš should throw the brick in order to hit his friend that is sitting in the same spot he was sitting. Is it possible that Aleš will not be able to do this? You should not account for any reaction time.

Some pills against flu dissolve in water making it to fizz. At first the pill is on the bottom of the glass but after a while it rises to the surface. Why?