Series 1, Year 19
Upload deadline: -, CET
1. can Saturn float?
Do you believe that average density of Saturn is lower than density of water?
You can look at Saturn in a telescope. Except the rings you will see several moon (if they are not behind Saturn in the moment – in such case you have to wait maximum 6 hours, which is the time of transit over the planet circle). You will find, that Titan orbits around Saturn once in 16 days. Can you calculate average density of Saturn from observation of Titan. If not, justify why and if yes, calculate it. You will notice one curiosity!
Při pozorování Saturnu vymyslel Pavel Brom.
2. train carriage
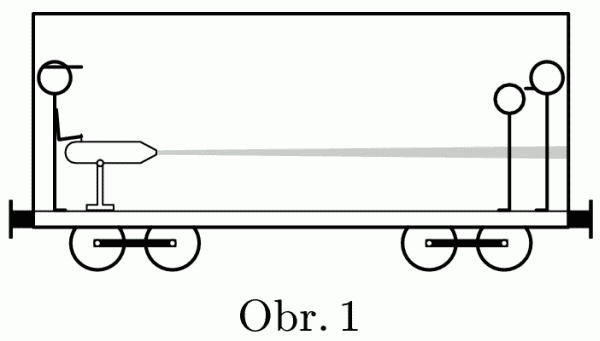
Imagine special anti-hooligan railway carriage equipped with a water cannon. The carriage weight is 30 t. Police (on the left) sprinkled hooligans with 1000 litres of water over 1 minute. How far had the carriage moved, if the wagon length is 30 m?
Assume that the carriage has brake off and that the water can escape only in vertical direction. The change in mass of carriage caused by escaped water can be neglected.
Zážitek Honzy Prachaře, když se vracel vlakem domů.
3. Armageddon
Alarm! Red lights indicate fatal threat. The meteoroid of know cross-section $S$ is approaching toward the Earth. Its thermal capacity is $c$. Calculate the increase of meteorite temperature during the flight through the atmosphere.
Assume, that its speed gets constant before impact and that it is heating uniformly. Estimate the part of energy which is used for heating the air in the atmosphere. Is this model realistic? Decide, if the meteorite will have higher or lower temperature if flying through the vacuum instead of air (vacuum has zero heat capacity).
Upravená úloha Kájinkova padajícího kulového kladívka.
4. get a loop
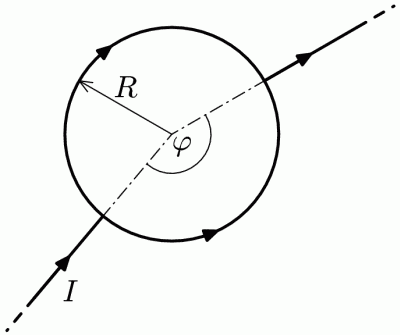
Assume circular loop made from wire. The current is fed by radial wires (see figure). What is the magnetic field in the middle of the loop? The radius of the loop is $R$, the angle between radial wires $φ$ and the current in the wire is $I$.
Navrhl Matouš.
P. tide on Bali
After the international physics olympiad on Bali all olympionics went relax to the beach on the south side of the island in Indonesia. They saw coral reef disappearing in the tidal wave and realized that, after full moon night and summer day, high tide happened only once (during 24-hour period). Aboriginals confirmed this observation, but could not explain it. Can you do it?
Honza na MFO na Bali.
E. hardness of balls
When you play marbles on autumn day, borrow few marbles and throw them against hard and flat surface. Then make a mark in the height where marble reached and measure it. From the measured values calculate coefficient of bounciness (ratio of energy before and after rebound).
Similar method is used for sorting hard/soft ball bearings. Soft balls do not bounce over barrier and are disposed.
Lenka
S. probability
- Three cards are randomly selected from 36 cards. Calculate probability of possibility that (i) just one ace was selected, (ii) at least one ace is selected and (iii) no ace is selected.
- $N$ identical particles is in a container. Calculate probability of case, that in the left part of container is $m$ particles more than in the right half. Draw a graph of dependence for $N=10^{10}$. Range of $m$ select so that the probability on the sides will be one tenth of the probability in the middle. How the width depends on $N?$ (Width is difference $m_{2}-m_{1}$, where $m_{2}>0$ a $m_{1}<0$ are values of $m$, for which the probability is half compared to the maximum).
- Estimate size of ln$n!$ (without using Stirling formula).
Autor seriálu Matouš.