Series 1, Year 18
Upload deadline: -, CET
1. duck on the pond
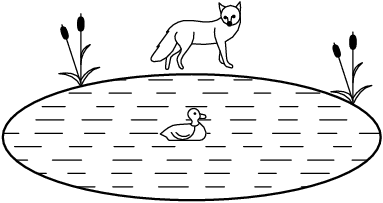
The duck is floating in the middle of the round pond. It wants to join others, unfortunately there is a fox on the bank. The duck cannot take of from water. It can take of only from the ground. Calculate the minimum ratio of the speeds of the duck and the fox for duck to be able to reach the bank and take off and not be eaten by fox. Suggest suitable strategy to reach this goal.
Někdo řekl Lence.
2. pendulum

Small ball is hanging at the end of mass-less string and oscillates around equilibrium (see figure) at frequency $f$. What will be its frequency $f'$ if the length of the string is half of original length?
MFO Kanada.
3. bricklayer
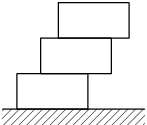
A bricklayer puts bricks as a stairs, one on each other. The aim is to build them as far as possible (horizontally) from the point where he started (where bricks are touching the ground). Suggest the strategy, which will give the longest reach! And, of course, no mortar/glue is allowed.
Navrhl Jarda Trnka.
4. water sprite
The water sprite (unterwasermann for German speakers) is sitting 1.5 meters under water level of his pond. How he sees the world above the water level? Assume, that refractive index of eye is same as refractive index of water.
Úloha ze sbírky prof. Vybírala.
P. anti-rocket
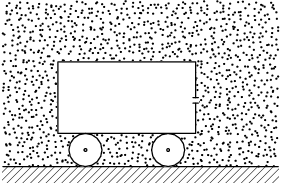
Assume a container on wheels with an orifice on the side. If the container is filled with compressed air, then the air escapes out and whole container moves. It is same principle as the rocket engines. Assume inverse situation – the container with vacuum inside in room full of air. How will the container move? The container can move without friction.
1. ročník 1.kolo.
E. and it spins!
It is few centuries since we know that the Earth spins around its axis. Measure the time, which is needed for the Earth to rotate 360° around its axis. Try to measure with highest possible accuracy. You can suggest and perform more than one experimental method. But, in each case do enough measurements to be able to do some statistic with the results.
Kolektivní výkon.
S. kinematics of point mass
* The position of point mass in time in Cartesian coordinates is described by position vector $\vect{r}(t) =(R \cos\(\omega t\)$,R sin\(\omega t\),d)\,.$$ Calculate, what is time dependence of vectors $v(t)$ and $a(t)$. Calculate tangential, normal and bi-normal component of acceleration.
- A wheel of radius $R$ rolls without slipping at straight track at velocity $v$. A point is connected with the wheel at the distance $r$ from the centre of wheel. Calculate its movement and the velocity as function of the time in coordinate system connected with the Earth. Can the speed be zero at some moment?
Autoři seriálu.