Series 2, Year 23
Upload deadline: -, CET
1. calamity
One of organizers of Fykos was travelling by train back home. The train was locked in by a snow storm. He was bravely counting snow flakes behind the window and was thinking: „How many snow flakes are in 1kg of snow?“ Are you able to make qualified guess to this question?
vzpomínáme na neznámého padlého
2. break the bridge
What is the optimum speed of walking person to put a bridge into a maximum amplitude? Define parameters needed and then solve.
Připomněl rotmistr Byrot.
3. barrel-organ
You can buy a roller on which surface a small bumps are located. The bumps then hit an edge of steel wafer, which have different length. In a song recorded on the roller you can find all tones in some interval (say, C major scale). Can you find out the shape of the wafers?
navrhl hudební guru Jakub M.
4. Marek's springs
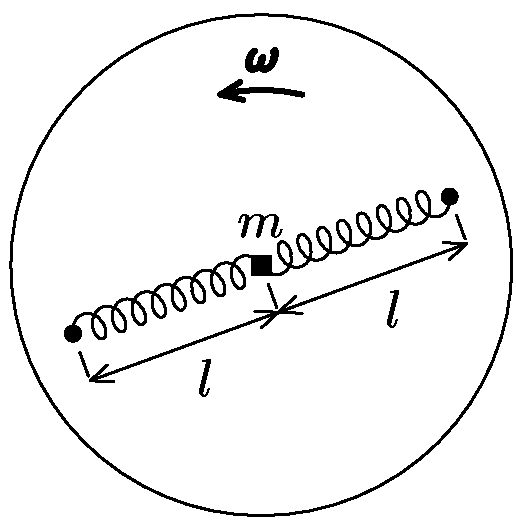
Marek made himself before Christmas a new toy: onto a wooden circle he put two nails (both nails and centre of circle in one line) and on two springs of stiffness $k$ he placed a weight of mass $m$. The weight can slide without friction on the surface of the wooden circle. Marek placed the circle onto a table and spin it around its axis with angular velocity $ω$, while the weight was slightly moved off the centre (equilibrium). Describe the movement of the weight, and as a bonus you can calculate it.
aniž by viděl náboj na soustředění, vymyslel Mára
P. telekinesis
Where does permanent magnet take the energy to lift stuff? We know, that magnetic force cannot do any work. Lorenz equation$\vect{F}$ = q ( \vect{v}\times \vect{B})$ says, that magnetic force is perpendicular to the velocity of moving charge and therefore only change its direction.
lámalo hlavu Honzovi Humplíkovi
E. metronome
If you play any musical instrument, then sometimes you experience problems with rhythm. Define an experiment and measure which frequency (knocking onto a table, pushing piano keys etc.) is easiest to keep. Is there any correlation between other natural effects?
Parkinsonem onemocněl Honza Hermann
S. mystery of overhead projector and fish-eye
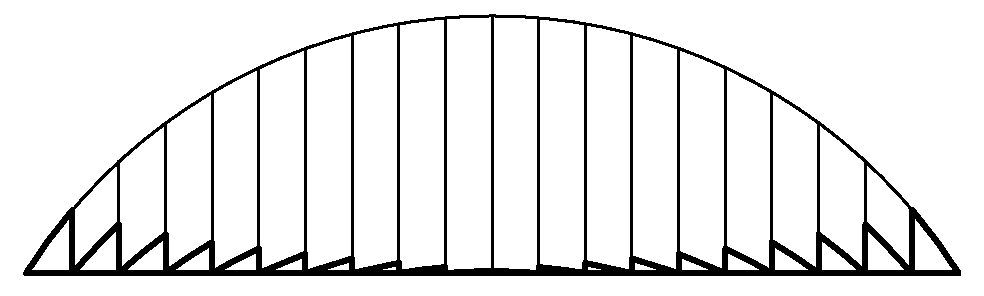
- You have maybe noticed, that in overhead projectors is often used very special lens, which looks more like a grooved plate. It is created in such way, that normal planoconvex lens is cut in concentric circles, the „end“ is kept and the result is again assembled. Finally we have axially symmetrical hilly glass (see figure).
Such lens has identical curvature to the original lens, and, according to Snell law we would expect, that will focus the light in the same way as original lens. However, looking at the situation using Fermat principle, the different beam paths do not experience the same time, as we have removed in different places different glass thickness. For example the shortest time is represented by the light beam travelling along the optical axis. It seems, that Fermat principle is failing, according it the lens should focus only the light following the optical axis and will not function as it should. Decide, who is correct: Snell or Fermat? And why?
- Find the path of beams in two-dimensional situation, when the dependence of refractive index is described by a function ($r$ is distance from the origin):
$n(r)=n_{0}⁄(1+(r⁄a))$.
- ( Bonus: If the point source of light is placed into the environment with varying refractive index, then some light can be focused into a single point, similar as in the situation of converging lens. This point is then called image of original point source. Describe the geometrical transformation from source to the image, which is induced by the environment from the previous question.
Z Kroniky Dalimilovy.