Series 3, Year 19
Upload deadline: -, CET
1. cylinder touching sphere
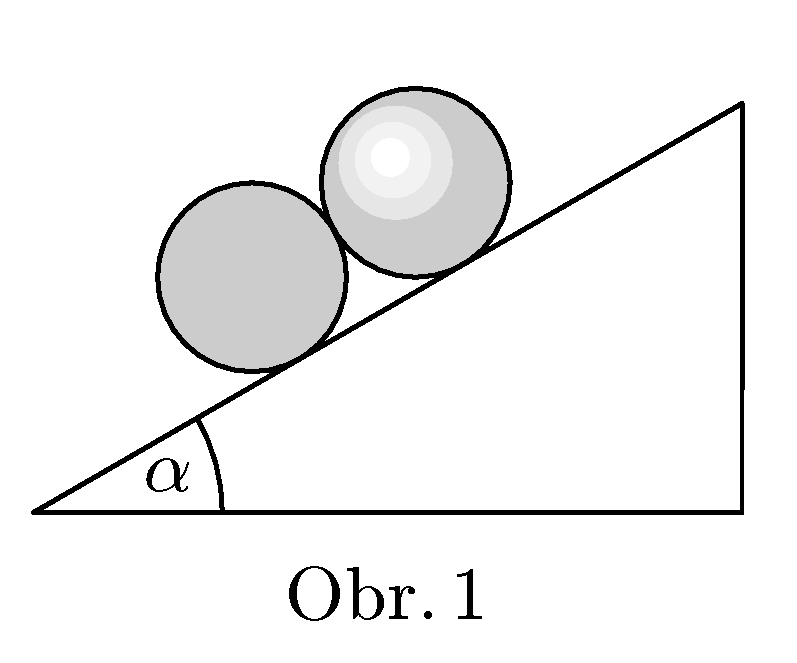
A cylinder and a sphere, both of the same radius and same weight are placed on inclined plane and are touching each other (see fig. 1). Determine, at which condition they will stay in rest.
Řešil Petr Sýkora při TJUFu.
2. raid at a lens
Lets have a lens of focal length $f$. The light source is at optical axis in distance $a>f$ from the lens. The light source starts moving at constant speed towards the lens. Calculate the speed of movement of the image of the light source. Decide, if this speed can be bigger than the speed of light. Would it contradict special theory of relativity?
Vymyslel Jarda Trnka, když psal studijní text z optiky.
3. delayed bath
Robin managed to get a bath full of hot water of temperature $T_{1}$ and volume $V_{1}$.
Robin's long-term dream was to isothemally compress gas of temperature $T$, volume $V_{0}$ and density $ρ$. And here it was an ideal occasion. As the cooler he used ambient air, which amount and heat capacity is unlimited and whose temperature is $T_{2}$. Calculate what is minimum volume $V$ to which he can compress the gas, if he uses only the warm water in the bath and newly constructed heat-engine.
Robin se nechal inspirovat na přednášce z termodynamiky.
4. rising current
A plane is flying horizontally at speed $v$ and suddenly enters into a rising current (jet) of speed $v′$. What will be acceleration of the plane just after entering the jet?
Assume the buoyancy coefficient $C$ (coefficient in Newton' equation for buoyancy) is linearly proportional to the angle between air flow and wing plane.
Navrhl Matouš Ringel, když mu úlohu odmítl prof. Volf.
P. breathless runner on ice
One winter day Matous went for a run on to frozen fishpond. After several meters he was not able to run any more and he stopped. The ice had broken under him. Explain, why it lasted when he was running!
E. vine analysis
Measure the alcohol content in cheap table vine and compare the content to the value declared on the packaging.
Našel Jarda Trnka na internetu a vzpomněl si při tom na jednoho z organizátorů.
S. application of statistical physics
- Using similar idea as in the case in theoretical text (sorry, only available in czech:-( ) calculate the form of Gultberg-Waage law for more complicated reactions (e.g. 2$A+B->A_{2}B)$. Try to find, if (and how well) this law follows reality.
- From Maxwell-Boltzmann distribution derive which power of temperature determine mean kinetic energy of particles of gas. Check, that you are able, using same method, find out dependence of any power of velocity on power of temperature.
- Lets have a system of independent spins, discussed in text, at temperature $T_{1}$, which is located in magnetic field $B_{1}$. Then the system is adiabatically isolated (i.e. is closed in to vacuum flask (thermos) to avoid any temperature exchange with environment) and the magnetic field is slowly reduced to value $B_{2}$. Explain, why the temperature of the system will decrease. Calculate final temperature $T_{2}$.
Hint: The work done on the system with magnetic moment $M$ at small change of the field $B$ of d$B$ is given by the equation d$W=-MdB$.
Autor seriálu, Matouš Ringel.