Series 6, Year 18
Upload deadline: -, CET
1. photoelectric effect
The cathode of photovoltaic cell is illuminated by the light from the mercury lamp of wavelength 546,1 nm. To eliminate photoelectric voltage, the voltage of $U_{1}=1,563V$ is needed. When the light has wavelength 404,7 nm, voltage $U_{2}=2,356V$ is needed. Calculate the value of Planck constant $h$.
Našel Honza Prachař v jedné sbírce.
2. how to make a black hole
When the star is compressed (or any other body) into a sphere of radius $r_{g}$, the black hole is created. So called Schwarzschild's radius $r_{g}$ can be interpreted in classical physics as a radius of a body of mass $M$, where the exit velocity is equal to the speed of light $c)$.
Knowing the mass of the star $M$ calculate Schwarzschild radius $r_{g}$ and critical density of the star $ρ$, at which it collapses into black hole. Solve for arbitrary values and then for the masses of Earth, Sun and the galaxy nucleus 100 billions heavier than Sun.
Jarda
3. space probe from NASA

In Jet Propulsion Laboratory in California, U.S.A. in NASA laboratory the new rocket engine is under development. It uses momentum of $α-particles$ created during radioactive decay of fermium $^{257}_{100}Fm_{157}$, which mass is $m_{Fm}$ and half-life $T$. The second product is californium $^{253}_{98}Cf_{155}$. The mass of $α-particle$ is $m_{α}$, the mass of californium is $m_{Cf}$, and during the decay the energy $E$ is released. Assume, that each $α-particle$ leaves rocket in the same direction.
The space probe with above engine is in rest at the beginning and its mass is $M$, the mass of 'fuel' is also $M$. Calculate the speed of the probe $v$ after half of the fermium decays. Resulting speed calculate also for the following numerical values $E=1,106\cdot 10^{-12}J$, $M=4\;\mathrm{kg}$ a $T=100,5days$, for other values consult your table-book.
SR olympiáda.
4. non-stoppable walker
Lets go back to Olympic games in Athens and determine maximum theoretical speed of the race walker. The walker is disqualified, if every referee (observer) agrees, that at least one leg was touching the ground in every moment.
Kdo jiný, než Matouš.
P. trip to Stonehenge
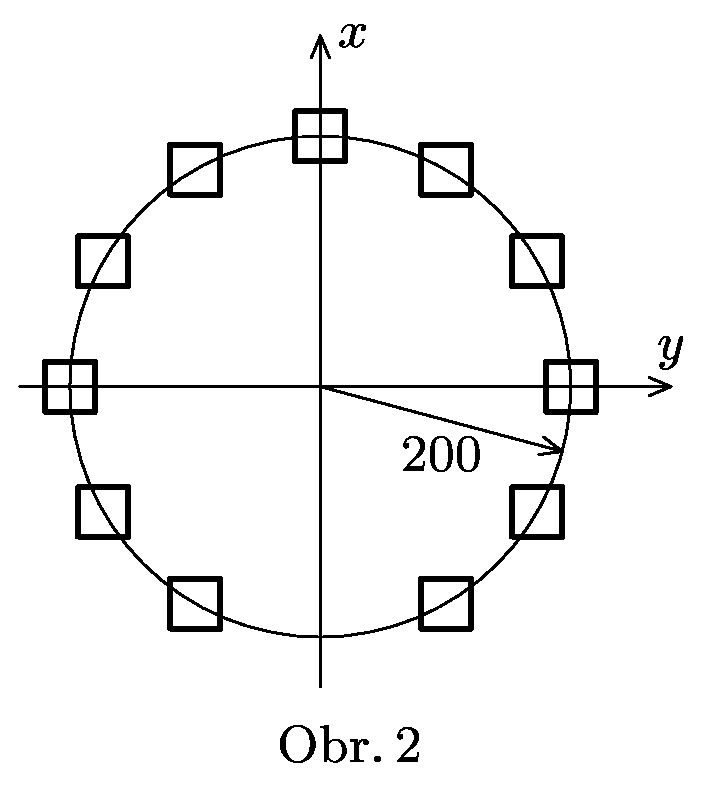
Imagine a trip in a rocket over Stonehenge. The Stonehenge is made from stone blocks in the the shape of regular dodecagon (object with 12 corners – see figure 2) of radius 200. You fly above the axis $x$ at the height $z=50$ and are looking in horizontal direction. When you are in the point of coordinates ( $-200$, $0)$ and ( 0$$, $0)$ you see the world exactly as in the image 6 respectively, while both of you have same eyes (at least the view angle:-). Calculate (approximately) the ratio of the speed of the rocket and the speed of light from the images.
Matous.
E. catch a photon
Measure the speed of light in vacuum. Use any method, for example use microwave oven.
Co jiného dát jak exp do roku fyziky.
S. Hamilton formalism
Lagrangian of a particle in electromagnetic field is
$L=\frac{1}{2}mv-qφ+q\textbf{v}\cdot \textbf{A}=\frac{1}{2}\;\mathrm{m}\cdot \sum_{i=1}^{3}v_{i}-qφ+q\cdot \sum_{i=1}^{3}v_{i}A_{i}$,
where $φ$ is electrical potential and $\textbf{A}$ is magnetic vector potential.
- Calculate generalized momentum of the particle $p_{i}$ belonging to the speed $v_{i}$.
- Write Hamiltonian function (in variables ($x_{i}$, p$_{i})!)$.
- Solve Hamiltonian equation, if when $\textbf{A}=**0**$ and $φ=-Ex_{1}$.
Zadal Honza Prachař.