Series 3, Year 18
Upload deadline: -, CET
1. temperature on the Earth
The average temperature at the earth is $T$ = 287 K. What is going to be the average temperature $T'$, if the average distance between the Earth and the Sun shrinks by 1%?
Část úlohy z 28. MFO v Kanadě.
2. bay watch
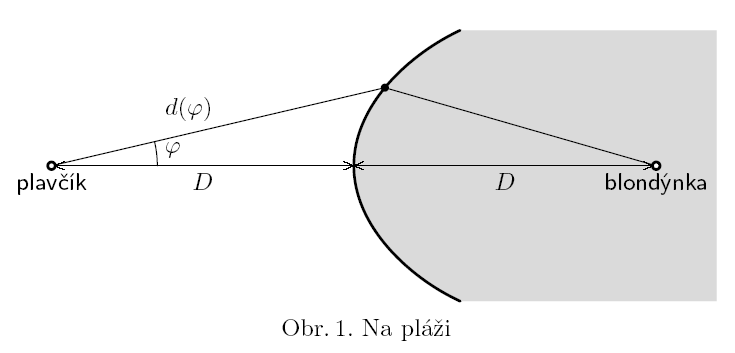
The lifeguard (plavcik) is standing in distance $D$ from the beach. He suddenly sees drowning blond girl (blondynka) which is in distance $D$ in sea (see fig. 1). The lifeguard can run at maximum speed $v$ and swim at maximum speed $v/2$. The distance from the lifeguard to the beach end is defined by following equation
$$d(\phi) = \frac{D}{3}( 8\cos{\phi}- {2\sqrt{16\cos^2{\phi}-12\cos{\phi} -3}}-3)\,,$$
where φ is angle blond-lifeguard-beach. What is the optimum trajectory for the lifeguard to safe her?
3. charged cube
What is the ratio of the electrostatic potentials in vertex and in the centre of non-conductive homogeneously charged cube? The total charge is $Q$, the edge length is $a$. Assume the electrostatic in infinity to be zero.
Vymyslel Pavel A.
4. with the glider over the channel

One of well known glider pilots decided to cross the British Channel. In Calais he rented a plane to took him to the height h = 3 km and from there glided directly to England. As every pilot knows, glider's downward speed $v_{kles}$ depends on the forward speed $v_{dop}$ as in the image 2. What is the optimum speed to achieve the longest flight? When the pilot is 3/4 of its way to England strong wind starts to blow in direction from England to France at the speed 10 $ms^{-1}$. What is the optimum speed now? What is the maximum wind speed which allows him to come to England? And what is the sped of wind to allow for the safe return to France?
Vymyslel Matouš.
P. the tower from push-carts
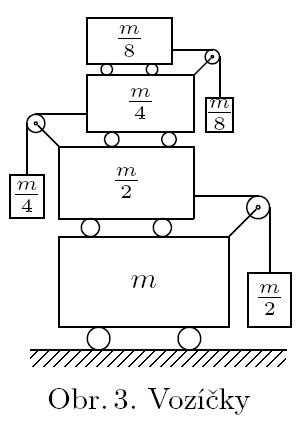
What is the acceleration of the first and hundred-th push cart on the image 3 (counting from the bottom)? There is infinite number of push-cars, on the image are depicted only first four. The mass of the bottom one is $m$, the second is $m/2$ and the mass of the weight attached is $m/2$ as well. The next mass is $m/4$ and the weight is $m/4$ etc. Assume that the weights are connected to the cars and are not moving in horizontal direction relatively to the carts. The friction between carts is negligible.
E. density of air
Measure the density of air. Use any method but do not forget to provide relevant theory. The correct answer should contain also estimation of experimental error.
S. Langrange's equations first type
- Lets have a mass point suspended on massless string. Introduce Cartesian coordinates and write down equation for the mass point.
- Write Lagrange's equations of first type for mass point from part a). Show, that they are equivalent with the equation for mathematical pendulum
d^{2}$\varphi/dt^{2}$ + $g/l$ \cdot sin $\varphi$ = 0,
where $\varphi$ is angular displacement from equilibrium.
- Small body is in rest at the top of the hemisphere and starts to slide down. Using Lagrange's equations for first type calculate the height when the body take-off the hemisphere. (
Hint: The body takes-off when the $λ$ = 0.)
Autoři seriálu.