Series 2, Year 22
Upload deadline: -, CET
1. rainbow
When and where on the Earth you cannot see a rainbow?
na schůzce vypotil Aleš
2. find the secret of calliper
Explain, how calliper (vernier caliper) works and how it is possible to measure up to 1/10th mm if the main scale is only 1mm!
nad tajemstvími života se zamyslel Marek Scholz
3. two balls
A small ball is at rest on bigger ball. The bigger ball is laying on the table without friction. We give a small impulse to the small ball and its will fall on the table. How far from the the original contact between table and large ball it will touch the table?
na teoretické mechanice zkoulel Lukáš Ledvina
4. into infinity and even further
An rich space-tourist has payed for a trip to the deep space. The Racket flies from the Earth and is accelerating with constant acceleration $a$, which can be verified by dropping a small ball. He is quite bored and therefore is watching disappearing Earth through the back window. After some time (how long it will take?) he starts to see, that something is not right. The Earth is not getting much smaller, and he deduces, that the space ship is slowing down, which does not correspond with the constant acceleration of $a$. However the tourist is not as good physicist and goes to file complain with captain. What should the captain to tell him?
Assume, that the tourist see whole electromagnetic spectrum and will survive the observation.
o prázdninách zkoušel Marek Pechal
P. lovers under the duvet
How will the temperature increase, if there are two person under duvet instead of one.
vymyslel zmrzlý milovník Honza P.
E. slanted PET bottle
How much of water has to be inside PET bottle placed upside down onto cap to make it the most stable (stability is defined as at small inclination bottle will fall in longest time). Do not forget to make theoretical assumption.
nad vypitou lahví se zamyslel Béda
S. Young and wave character of light
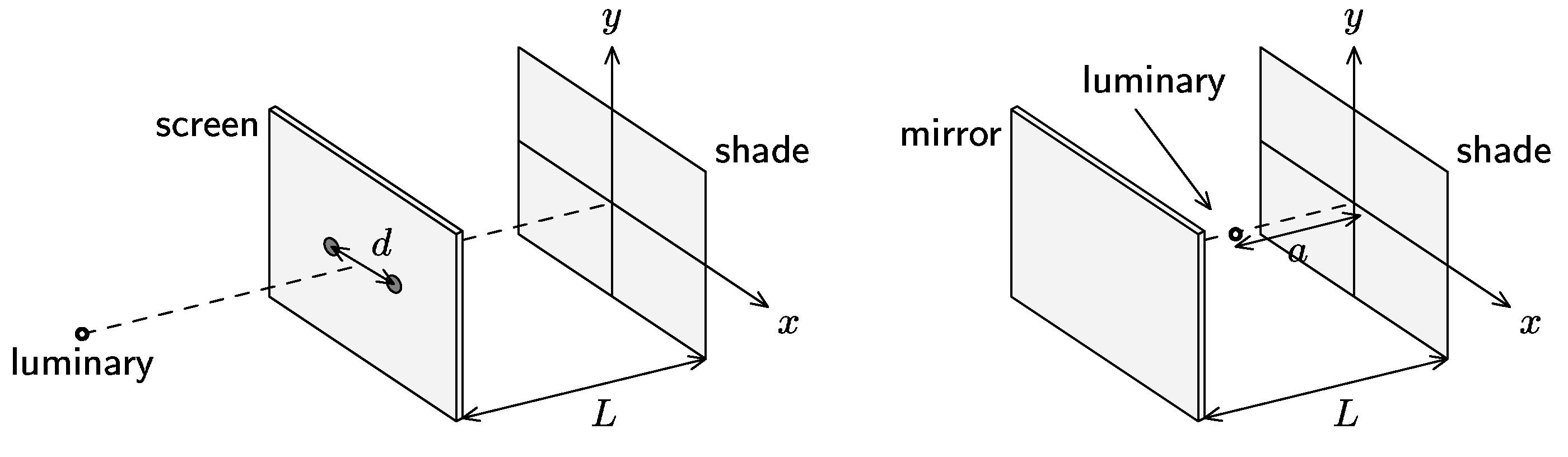
Situation
- What shape of interference pattern would you expect in following two configurations? Find the equations of curves of maximum intensity and try to plot some of them.
- Show, how the experiment should end, if the light behaves according to Newton assumptions. Do consider different angle of incidence at different places on the screen.
- Using quantum-mechanical description find resolution, which should have get Jöhnsson by using 4 slits (4 parallel orifices in distance $b$ between neighbouring slits. Plot representative part of the graph and comment advantages of higher number of orifices.
Autoři seriálu