Series 4, Year 30
Upload deadline: Upload deadline: 28th February 2017 11:59:59 PM, CET
(3 points)1. princess Point on point
It is not easy for story characters if they want to know when they appear on screen. Fortunately, today's technology makes it easier, take for example princess Point from a story with six chapters. All chapters have the same length with the height of every chapter on Karel's display being 1200 pixels (but the display itself can only show 900 pixels at any one time). When reading Karel scrolls continuously and reads with constant speed. After three minutes of reading, Point passed the first end of the slider in the scrollbar and after seven minutes she passed the other end. Which chapter does Point appear in? Note: The ratio of the height of the slider and the height of the display is the same as the ratio of the height of the display to the height of the entire story.
Michal's scrollbar was slipping.
(3 points)2. jerky pendulum
It is well known fact that to make a train ride as comfortable as possible, when accelerating or braking, the acceleration needs to change as little as possible. It is therefore good practice when a train starts with small, constant change of acceleration. The change of acceleration is called a jerk. Determine how does the equilibrium position of a pendulum (the angle with the vertical $φ)$. Denoting the length of the pendulum $l$, the train starts with a constant jerk $k$ ( $k=Δa⁄Δt$, where $a$ denotes acceleration) and the train is on Earth with acceleration due to gravity $g$. Bonus: Derive the equations of motion and solve them numerically for $φ(0)=0$ and $dφ⁄dt(0)=0$ for various values of $k$.
Occurred to Karel when he should have been writing his thesis.
(8 points)3. bicone
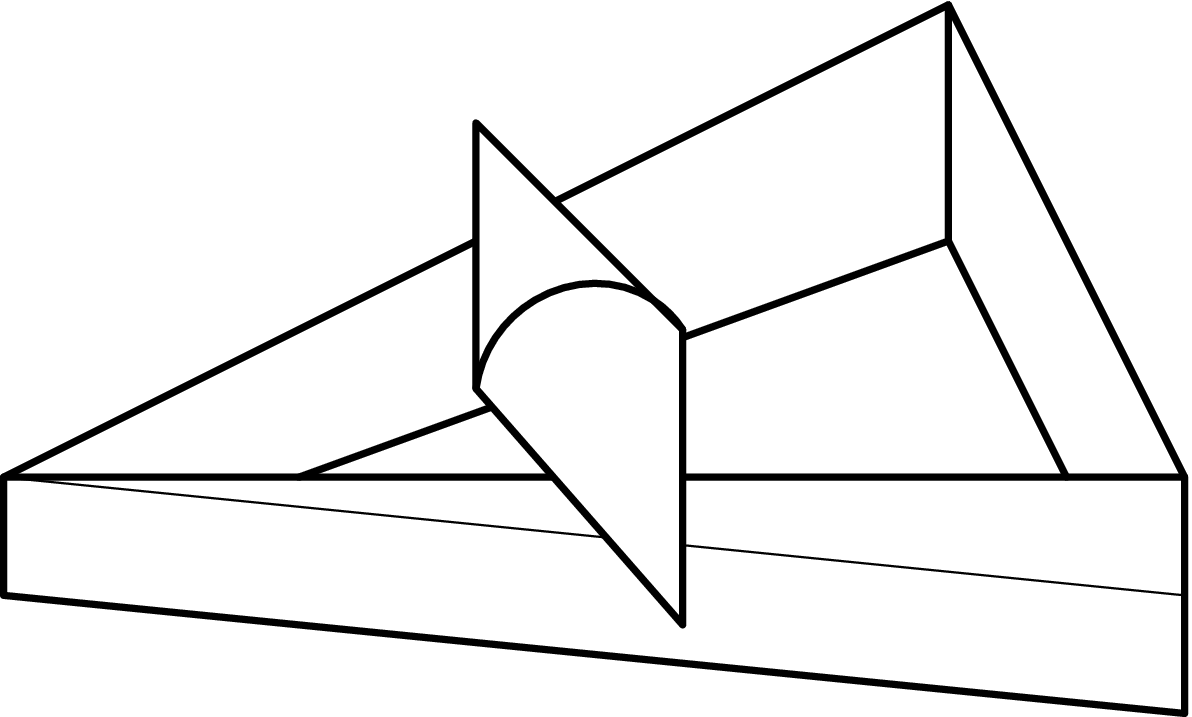
Consider a wooden construction (shown in the picture) with its foundation in the shape of an isosceles triangle with a base of length $c=35\;\mathrm{cm}$. The height of the legs of this triangle increases towards the base with an angle $α=2°$ with the flat ground. A bicone with opening angle $φ=40°$ and height 2$h=40\;\mathrm{cm}$ is placed in the vertex opposite the base, where the triangle has angle $β=70°$. When released, the bicone starts rolling „uphill“, that is in the direction of the increasing height of the legs.
- Explain why the bicone can roll uphill.
- Find the dependence of the position of the centre of mass on the distance covered by the bicone?
- What is the velocity of the bicone in the instant before it hits the base.
- How many turns will the bicone make before it hits the base? The bicone is initially placed horizontally on the construction in such a way that its centre of mass is exactly above the vertex opposite the base.
Conic sections in linear algebra reminded Mirek about this nice experiment.
(8 points)4. heat engine
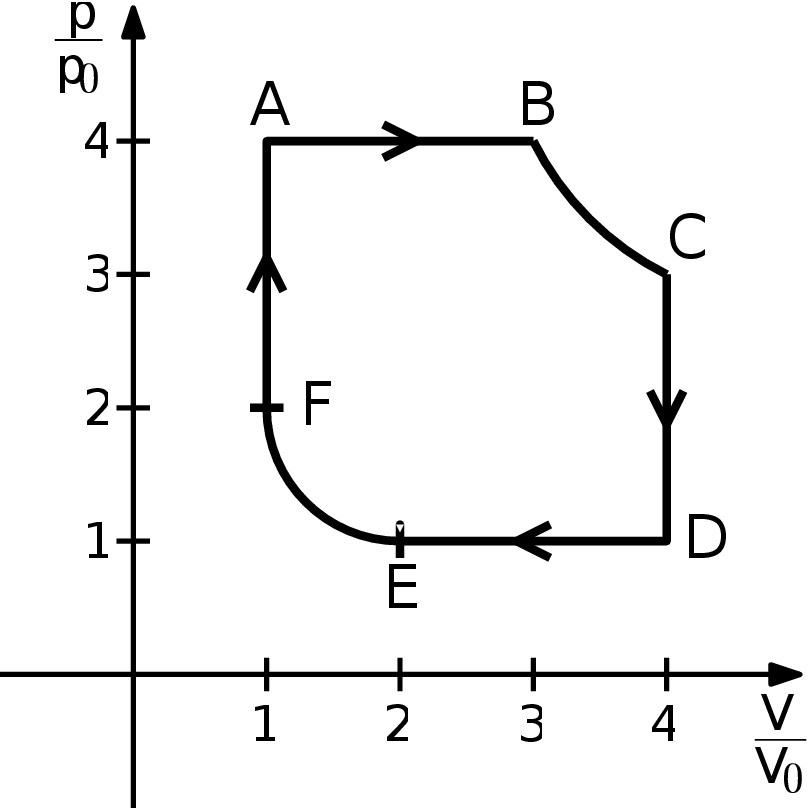
Consider a heat engine filled with a diatomic gas. This engine works thanks to a cycle ABCDEFA as shown in the picture. The 6 processes that make up the cycle are
- A $→$ B - isobaric heating from a state 4$p_{0}$ and $V_{0}$ (let us denote temperature at A 4$T_{0})$ to a state with volume 3$V_{0}$,
- B $→$ C - isothermic expansion to volume 4$V_{0}$,
- C $→$ D - isochoric cooling to pressure $p_{0}$,
- D $→$ E - isobaric cooling to volume 2$V_{0}$,
- E $→$ F - isothermic compression to volume $V_{0}$,
- F $→$ A - isochoric heating to pressure 4$p_{0}$. Determine the remaining state variables in B, C, D, E, and F, the maximal and the minimal temperature of the ideal gas during the process (as a multiple of $T_{0})$, heat received and lost by the gas in each process, and the overall efficiency of the engine. Compare this efficiency with that of a Carnot engine working between the same minimal and maximal temperatures. Assume for simplicity that the molar amount of the gas does not change and there are no chemical changes during the cycle. A sketch can be seen in figure.
Bonus: Do the same for a much simpler „square“ cycle, ABCDA, where the gas starts in a state $p_{0}$, $V_{0}$ and $T_{0}$ and izochorically heats up to 4$p_{0}$, isobarically heats up and expands to 4$V_{0}$, isochorically cools down to $p_{0}$ and isobarically cools down to $V_{0}$. Compare the efficiency of these two heat engines and suggest which one is better.
Karel was alternately warm and cold
(9 points)5. weird atmosphere
Have you ever seen such a weird atmosphere? Up to a certain height the speed of light inside it is constant, $v_{0}$, but from that certain height the speed of light starts increasing linearly as $v(Δh)=v_{0}+kΔh$. At one point, exactly at the height where the speed of light starts changing, light beams are sent upward in all directions. Show that all these beams move along circular arcs and determine the radii of these arcs. Also find out the distance between the place where the the light was emitted and the point where the beams return to the original height.
Jakub wanted to know what it would be like to swim under ice.
(9 points)P. statistician's daily bread
We've all been there, you spread some honey or some preserve on a slice of bread, take a bite, and suddenly, the spread drips through a hole and lands right on your hand. Determine how does the probability that there is a hole straight through a slice of bread depend on its thickness. The model of how does the dough rise is left up to you. (For example, evenly distributed bubbles with an exponential distribution of radii is a good model).
Michal stained his clothes.
(11 points)E. Mikulas's egg
Measure the surface area of a bird's (e.g. chicken's) egg.
Mikulas made pancakes.
(10 points)S. testing
- Try to describe in your own words what purpose serves testing of hypotheses and how its done (it is sufficient to briefly describe the following: null hypothesis and alternative hypothesis, type I and type II error, level of significance, test statistic, confidence level, $p$-value). It’s not necessary to describe the concepts mathematically, a brief description in your own words is sufficient.
- In the attached data file testovani1.csv there are measurements of a certain physical quantity. Using one-sample $t$-test find out whether the real value of the measured quantity is equal to $20$. Then suppose our aim is to show that the real value is larger than $20$. Test this claim using an appropriate modification of $t$-test (be careful which null hypothesis and alternative hypothesis you choose).
- In the attached data file testovani2.csv you may find the measurements of two different physical quantities. Assume the measurements to be of the same physical characteristic, just under different conditions (temperature, pressure etc.). Test the hypothesis that the value of said physical characteristic is the same under both sets of outside conditions using the two sample $z$-test.
- Use the data from the last task in the first series of this year and using Kolmogorov–Smirnov test determine which of the four data samples comes from uniform distribution and which comes from exponential distribution.
Bonus: Assume you have at your disposal measurements of 2 physical quantities (i.e. two sets of measurements), where all the data are independent. Set up a modified $z$-test, that will test the hypothesis that the real value of the first physical quantity is double the real value of the second physical quantity. It is sufficient to set up the corresponding test statistic and confidence level. (Hint: Use the multidimensional central limit theorem with appropriately selected function $f$, and then proceed analogically to setting up a classical two-sample $z$-test) For data processing and creating the plots, you may use the R programming language. Most of these tasks can be solved by slightly altering the attached scripts.
Michal wanted to test, how difficult problems you can solve.