Series 3, Year 31
Upload deadline: Upload deadline: 9th January 2018 11:59:59 PM, CET
(3 points)1. slowed down
Let's suppose a camera with a frame rate of 24 frames per second (consider evenly spaced and perfectly sharp shots). We record a flight of a helicopter with the rotor rotation velocity of $2 900 \mathrm {cycles/min}$. Then the record is played. What is the apparent rotational velocity of the rotor in the record?
(3 points)2. small acceleration, large acceleration
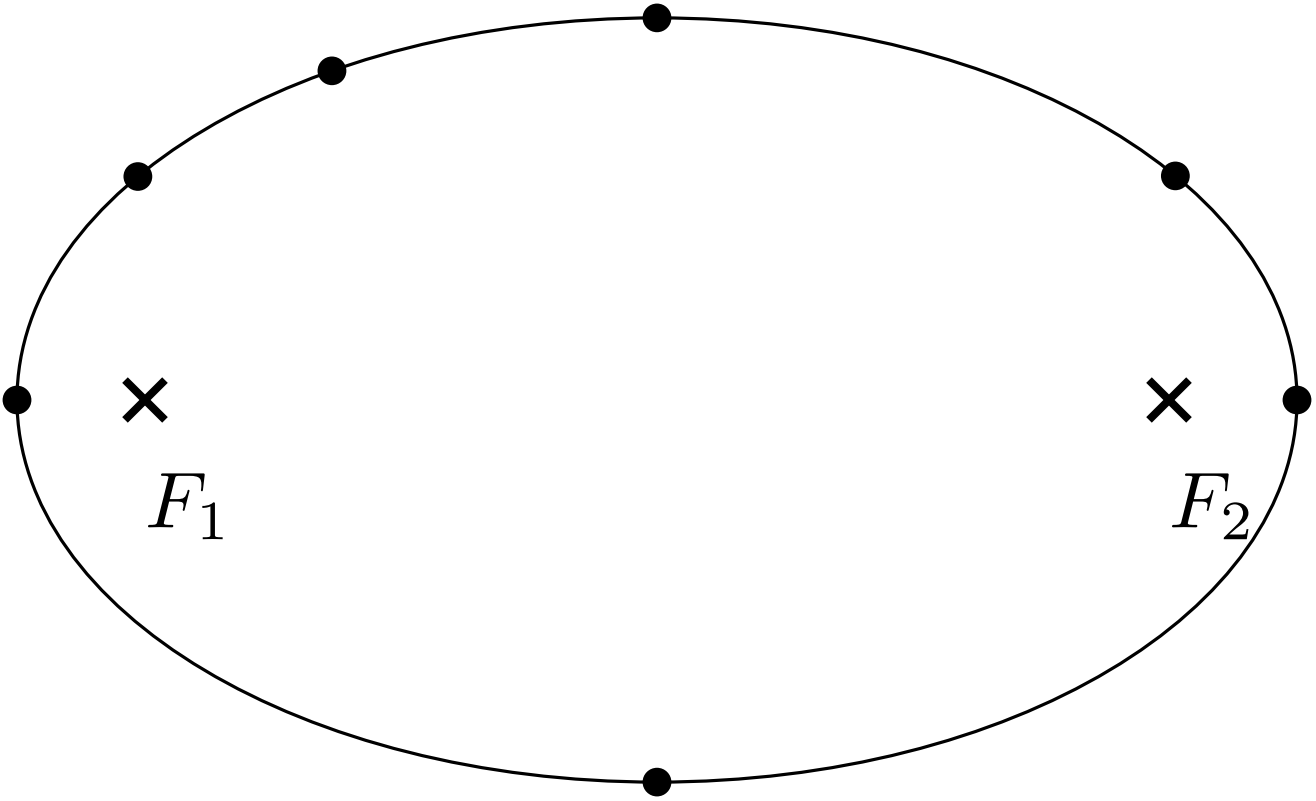
The ellipse
In the figure, there is an ellipse with two focal points $F_1$ $F_2$ and several marked points on the ellipse. The ellipse represents a trajectory of one material point. Plot the accelerations the point experiences in given points of its trajectory. Show it in a figure. The direction and ratio of accelerations are important.
- There is a massive body in the focal point $F_1$. The material point is orbiting it, and Kepler's $2^{\rm nd}$ law applies.
- The absolute value of velocity of the material point is constant. It only moves along the ellipse.
(6 points)3. IDKFA
You fired at Imp from your plasma gun which shoots a cluster of particles with uniform velocity distribution in interval $\langle v_0, \; v_0+\delta v\rangle$ (all of the particles are moving in one line, there is no transverse velocity). The total kinetic energy of the cluster is $E_0$. The barrel rifle has a cross cestion of $S$ and the pulse takes an infinitely short time. How far does Imp need to stand to be safe. Assume that his skin is able to cool the heat flow of $q$.
(7 points)4. dropped pen
We drop a pen (rigid stick) on a table so that it makes an angle $\alpha $ with horizontal plane during its fall. Calculate the velocity of the higher end during its impact. When we dropped the pen, its center of mass was at height $h$. All collisions are inelastic and friction between the table and the end of the pen large enough.
Bonus: Calculate the angle $\alpha $ so that the velocity (of the second end that touches the table) is maximal. For which height $h$ is it worth to tilt the pen?
Matt was bored.
(8 points)5. decay here, decay there
We have $A_0$ particles which decay into $B$ particles with decay constant $\lambda \_A$. $B$ particles decay into $A$ particles with decay constant $\lambda \_B$. The number of $B$ particles at the beginning is $B_0$. Find a ratio of the numbers of particles $A$ and $B$ as a function of $t$.
(8 points)P. folded paper
Everyone has certainly heard and surely tried it: „Sheet of paper can not be folded in a half more than seven times.“ Is it really true? Find boundary conditions.
Kuba was bored and folded a paper.
(12 points)E. magnetically attractive
You got a planar magnet (magnetic foil) together with the tasks of these series. This magnet is a bit different than a rod magnet. The south and north poles are alternating parallel lines. When approaching the ferromagnetic surface, a magnetic circuit is created which holds the magnet (for example, on the fridge) and can carry even a picture on itself. Your tasks are:
- Measure the area and thickness of the film which you be used for your experiments.
- Measure the mean distance between the two closest same magnetic poles (twice the distance of opposite poles).
- Measure the maximum payload (ie. weight without magnet weight) which can be carried by a $1 \mathrm{cm^2}$ of a magnet if the magnet load is even if the magnet is attached to the bottom of the horizontal plate. The plate should be approx. $1 \mathrm{mm}$ thick sheet made of magnetically soft steel.
Charles obtained a magnetic foil.
(10 points)S. a walk with integrals
- Propose three different examples of Markov chains, at least one of which is related to physics. Is a random walk without backtracking (a step cannot be time reversed previous step) an example of Markov chain? What about a random walk without a crossing (it can lead to each point at most once)?
- Consider a 2D random walk without backtracking on a square grid beginning at the point $(x,y) = (0,0)$. It is constrained by absorbing states $b_1\colon y = -5$, $b_2\colon y = 10$. Find the probability of the walk ending in $b_1$ rather than in $b_2$.
- Simulate the motion of a brownian particle in 2D and plot the mean distance from the origin as a function of time. Assume a discrete time and a constant step size. (One step takes $\Delta t = \textrm{const} $, and the step size is $\Delta l = \textrm{const} $). A step in any arbitrary direction is possible, i.e. every step is described by it’s length and an angle $\theta \in [0,2\pi )$, while all directions are equally probable. Focus especially on the asymptotic behavior, i.e. the mean distance for $t \gg \Delta t$.
- Error function is defined as \[\begin{equation*} {erf}(x)=\frac {2}{\sqrt {\pi }}\int _0^x \eu ^{-t^2} \d t . \end {equation*}\] Calculate the integral for many different values of $x$ and plot it’s value as a function of $x$. What do you get by numerically deriving this function?
- Look up the definition of Maxwell-Boltzmann probability distribution $f(v)$, i.e. the probability distribution of speeds of particles in an idealized gas. Utilizing MC integration calculate the mean value of speed defined as \[\begin{equation*} \langle v\rangle = \int _0^{\infty } vf(v) \d v , \end {equation*}\] Use the Metropolis-Hastings algorithm for sampling the Maxwell-Boltzmann distribution. Compare the values of particular parameters with the values from literature.
Mirek and Lukáš random-walk to school.