Series 2, Year 26
Upload deadline: -, CET
(2 points)1. from Prague to Brno
Assume that the Earth is a sphere and the surface distance between Dresden and Vienna is approximately $d=370$ km. How much is the distance reduced if you decide to dig a tunnel between those two cities instead of walking. Neglect the different altitudes. Compare the tunnel distance with walking distance. For simplicity, you can approximate trigonometric functions as $$ \mathrm{sin} α ≈ α - α^{3}/6 \,,\\ \mathrm{cos} α ≈ 1 - α^{2}/2 \,,\\ \mathrm{tg} α ≈ α + α^{3}/3 \,, $$ where the angle is assumed to be given in radians.
(2 points)2. hollow Earth
Imagine that all the mass of the Earth is remodeled into a spherical shell. The thickness of the shell is $d=1\;\mathrm{km}$. Assume the density remains the same, what is the outer radius of the new planet? What is the gravitational acceleration on its surface?
(4 points)3. life in Venice
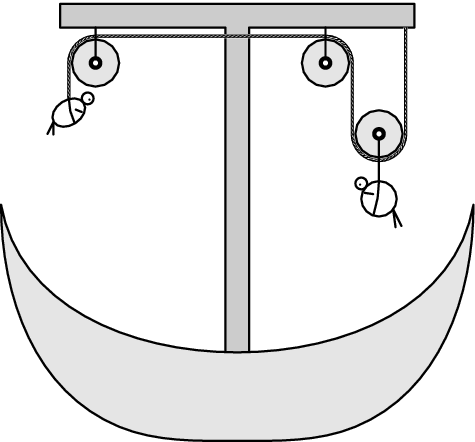
Two chubby residents of Venice Paolo and Francesca Muschetti (with masses $m_{P}=180\;\mathrm{kg}$ and $m_{F}=130\;\mathrm{kg})$ decided to go for a gondola ride. However, none of the gondoliers would allow them to enter the boat because it would sink. Fortunately, they managed to find one gondolier who designed the device shown on the picture. Both Paolo and Francesca were tied to the ends of the rope in such a way that at first Francesca was at the top but then she switched with Paolo. How tall should this device be in order for the boat to traverse the canal? The travel time is $τ=60\;\mathrm{s}$. Assume that if this device is used, the gondola does not sink. You can neglect any friction, the mass of the rope and the moments of inertia of all the pulleys.
(5 points)4. a hamster
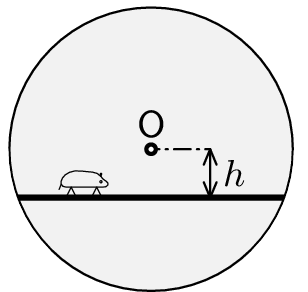
Imagine the toy for hamsters depicted in the picture. The cylinder is free to rotate around the center point $O$. The hamster stands on the horizontal plate that is glued to the cylinder at a distance $h$ from the axis of rotation. How should the hamster move in order for the plate to stay in the horizontal position? The coefficient of friction between the hamster and the plate is $f$.
(5 points)5. the U tube

Imagine a U-tube filled with mercury, and a bubble of height $h_{0}$ that floats inside (see the attached picture). Describe what would happen if we changed the surrounding atmosphere in the following ways. Assume that the density of mercury is independent of temperature. The same is valid for the glass the tube is made of. Also assume that the surrounding air behaves as an ideal gas. The initial state of the atmosphere is described by temperature $T_{0}=300K$, and pressure $p_{a}=10\cdot 10^{5}Pa$. Furthermore, assume that the system is in a thermodynamic equilibrium at all times, and that the bubble has a cylindrical shape.
- Both ends of the tube are open, and the temperature doubles.
- Both ends of the tube are closed, and the temperature doubles.
- Only one of the ends of the tube is closed, and the temperature doubles. For each of these cases, determine the new size of the bubble, and the height difference between the mercury columns in the two branches.
Bonus: Repeat the calculation assuming that the volume of mercury grows linearly with temperature.
(5 points)P. messing with gravity
What if the gravitational constant suddenly doubled (without affecting the value of other physical constants)? What if it increased a hundred times? Discuss the impact the change would have on the life on the Earth and on the trajectories of bodies in the universe.
(8 points)E. it's fall again
Estimate the average surface area of a leaf of your choice. We are looking forward to see a thorough statistical analysis of your measurements! Use your result to estimate the fraction of energy obtained from the Sun that is used to make saccharides.
(6 points)S. drifting
- What kind of drifts can we observe in a linear trap? Assume that the axis of the trap is horizontal. Will the drift caused by the gravitational force have a significant effect on the motion of a particle?
- Derive a formula for the loss cone and draw an original picture illustrating the behavior of a particle in a linear trap.
- Derive a formula for the drift caused by an electric field that is perpendicular to a magnetic field and that has a constant gradient parallel with the electric field. Discuss the the dependence of the particle trajectories on the magnitude of this gradient.