Series 5, Year 27
Upload deadline: -, CET
(2 points)1. a pressured giraffe
Compare the blood pressure in the head of an adult giraffe and an adult human $p_{h1}=120\;\mathrm{mm}Hg$ and in the giraffe $p_{g1}=280\;\mathrm{mm}Hg,the$ density of the blood of both animals is $ρ=1050\;\mathrm{kg}\cdot m$. Consider only the case where both the human and giraffe are standing. The speed of the flow of the blood is to be assumed constant.
Mirek was wondering why a giraffe doesn't faint.
(2 points)2. uranium star
Imagine that no thermonuclear fusion occurs in stars and instead they run on nuclear fission. Estimate how long such a star would be able to shine if at the beginning of its life cycle it is composed of uranium 235, its mass and luminosity are both aproximately constant and are equal to the current values of the sun.
Mirek was reading through his new textbooks.
(3 points)3. the fine container
Consider a cylindrical container which fills the volume of $V=1l$. The container is closed with an airtight moving piston which has a non-negible mass $M$. Furthermore we know that the container is divided by horizontal partitions into $n$ sections and in the $i-thsection$ (it is numbered from the top ascendingly) there are 2^{$i}a$ particles, where $ais$ an undefined constant.The partitions are not fixed with regards to the container but at the same time they prevent the sections in which the ideal gas can be found from exchanging heat or particles. The whole system is at equilibrium. Then we make the mass of the piston twice as large and wait for equilibrium to arise again. How will the volume of the gas in the container change? Do not consider atmospheric pressure.
Nahry was under pressure and created a problem about pressure.
(4 points)4. Trianglular resistor
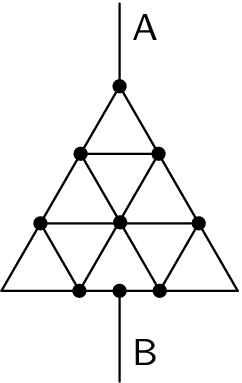
Determine the resistance of a triangle created out of resistive wires between clamps A a B, that you see in the picture. One side of the small triangle (of which the bigger triangle is composed of) has the resistance of $R_{0}.Neglect$ the resistance of the wires that led it there.
Karel was drawing triangles
(5 points)5. Babysitting
Consider a swing held up by two ropes of length $l=1.5\;\mathrm{m}$ that hang from a pole of radius $r=4\;\mathrm{cm}$. The child sitting on the swing shall gain in the bottom dead center such a speed $v_{0}$ that the child shall accomplish a whole turn around the horizontal pole and that the ropes shall be experiencing a tension sufficient enough for them to be rigid throughout the turn. At the same time we wish to minimalize the initial velocity. Determine the difference of the angular velocity $ω_{1}of$ the swing with the child after its return to the bottom dead point and the initial angular velocity $ω_{0}$.
Hint: To calculate the centripetal acceleration you may assume that locally the child is moving on a circular path.
Mirek always liked playing with his younger siblings.
(5 points)P. physics in flames
On what physical (or chemical) values does the temperature at which a certain material burns depend? How does it depend on them? Determine such a temperature for one such material.
Karel was musing about flames
(8 points)E. rubbery
An object of mass $m$ on a piece of rubber of length $l_{0}is$ hung at a rigid point, the coordinates of which are $x=0$ and $y=0$. From the $xaxis$, which is horizontal, we slowly release the mass. What will be the relation between the lowest point reached and its position on the axis $x?$
Dominika was testing which method is optimal for gouging someone's eyeball out.
(6 points)S. string
- We consider only open strings and we shall limit ourselves merely to three dimensions. Draw how the following things look like
- a string moving freely through timespace,
- a string fixed with both ends to a D2-brane,
- a string between a D2-brane and D1-brane.
Where can the strings end in the case of three parallel D2-branes?
- Choose one of the functions
$$\mathcal{P}_{\mu}^{\tau}$$
ot $$\mathcal{P}_{\mu}^{\sigma}$$ that was defined in the first part of the series and find its explicit
form (in other words a direct dependence on $$\dot{X}^{\mu}$$ and <img
src=„https://latex.codecogs.com/gif.latex?X'^{\mu}“>). Show that the conditions $$\vect{X}'\cdot \dot{\vect{X}}=0$$
and $$|\dot{\vect{X}}|^2=-|\vect{X}'|^2$$
- Find the spectrum of energies of a harmonic oscilator.
- The energy of the oscilator is given by the hamiltonian
$$\hat{H}=\frac{\hat{p}^2}{2m} \frac{1}{2}m\omega^2\hat{x}^2$$
The second expression is clearly the potential energy while the first gives after substituting in $$\hat{p}=m\hat{v}$$ kinetic energy. We define linear combination as
$$\hat{\alpha}=a\hat{x} \;\mathrm{i} b\hat{p}$$ . Find the real constants <img
src=„https://latex.codecogs.com/gif.latex?a“> a $b$ , such that the Hamiltonian will have the form of
<img src=„https://latex.codecogs.com/gif.latex?\hat{H}=\hbar \omega \left(\hat{\alpha} ^{\dagger}\hat{\alpha}+\frac{1}
{2}\right)\,,“> where $$\hat{\alpha} ^{\dagger}$$ is the complex conjugate <img
src=„https://latex.codecogs.com/gif.latex?\hat{\alpha}“>.
- Show from your knowledge of canoninc commutation relations for
$$\hat{x}$$
and $$\hat{p}$$ that the following is true
<img src=„https://latex.codecogs.com/gif.latex?\left[\hat{\alpha},\hat{\alpha}\right]=0\,,\quad\left[\hat{\alpha} ^{\dagger},\hat{\alpha} ^
{\dagger}\right]=0\,,\quad\left[\hat{\alpha} ,\hat{\alpha} ^{\dagger}\right]=1\,.“>
- In the spectrum of the oscilator there will surely be the state with the lowest possible energy which corresponds to the smallest possible
amount of oscilating. Lets call it $$|0\rangle$$ . This state must fulfill <img
src=„https://latex.codecogs.com/gif.latex?\alpha |0\rangle =0“>. Show that its energy is equal to $$\hbar\omega/2$$ , ie. $$\hat{H}|0\rangle=\hbar\omega/2|0\rangle$$ . Furthermore prove that if $$\alpha |0\rangle \neq 0$$ then we have a contradiction with the fact that <img
src=„https://latex.codecogs.com/gif.latex?|0\rangle“> has a minimal energy ie. <img src=„https://latex.codecogs.com/gif.latex?\hat{H}\alpha |0\rangle=E\alpha
$$E<\hbar\omega/2$$ . All the eigenstates of the Hamiltonian can be described
as $$\left(\alpha^{\dagger}\right) ^n|0\rangle$$
for $$n=0,1,2,\dots$$ Find the energy of these states, in other words find such numbers <img
src=„https://latex.codecogs.com/gif.latex?E_n“> that <img src=„https://latex.codecogs.com/gif.latex?\hat{H}\left(\alpha^{\dagger}\right) ^n|0\rangle=E_n\left
(\alpha^{\dagger}\right)^n|0\rangle“>.
Tip Use the commutation relation for $$\hat{\alpha}^{\dagger}$$ a <img
src=„https://latex.codecogs.com/gif.latex?\hat{\alpha}“>.