Series 4, Year 25
Upload deadline: -, CET
(2 points)1. stairs from Chrudim
Escalators at the subway station Náměstí Míru consist of $n$ steps and move with speed $v$. How many times do you actually have to step before you reach the end if you move a) in the same direction as the escalator, b) opposite to the direction the escalator moves. Assume that you move with speed $v_{1}$ such that $v_{1}>v$.
Aleš po cestě do otevřených dveří.
(2 points)2. Gatling gun
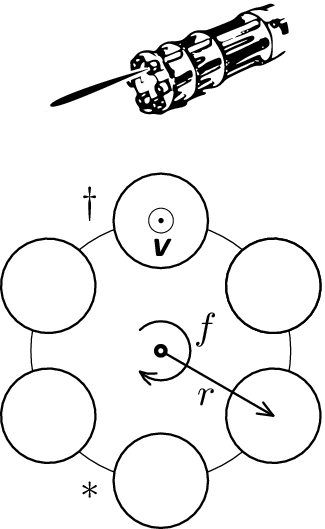
At first developed as an equipment that would simplify the distribution of seeds, gatling gun turned out to be much more useful for distributing bullets. Relative to the gatling gun's barrel, what is the region where you are in danger of being shot? The calibre is $d$, number of barrels $n$, distance from the barrel's axis to the axis of the shaft is $r$, the gun can make $f$ rotations per second, firing rate is $F$ and a bullet leaves the barrel with speed $v$.
Napadlo Michala při čtení tajného časopisu.
(3 points)3. flying stone
How long will it take for a spherical stone of mass $m$ to reach the bottom of a pond $d$ meters deep if you throw it in from height $h?$ How will the answer change if the stone is „flat“ and not spherical?
Dominika házela šutry.
(4 points)4. rockets
Model of a rocket contains a motor whose power output is constant as long as it is provided with fuel. The initial mass of the fuel is $m_{p}$, the mass of an empty rocket is $m_{0}$ and the amount of fuel burned by the motor grows linearly with time. What is the maximum height the rocket can reach assuming the gravitational field to be homogeneous and the air resistance to be negligible?
Michal odpaloval rakety.
(4 points)5. gas leakage
What is the mass percentage of Earth's atmosphere that escapes to the outer space each year? Assume the atmosphere reaches 10 km above the ground, the pressure is everywhere the same (equal to the pressure at sea level) and it consists of ideal gas at tepmperature 300K whose molecular speeds obey the Maxwell-Boltzmann distribution. Also assume that the gravitational field is homogeneous.
Aleše napadlo při úniku.
(5 points)P. energy saving
Some apartment buildings have only one boiler that is used by all the tenants. The way the boiler works is that it keeps the water temperature constant throughout the day. In order to save money the tenants decided to turn off the boiler every night and turn it back on the next morning. Therefore every morning the boiler has to heat up the water that cooled down during the night. Estimate how much energy is saved by this method and suggest a better way to save money without making the living more uncomfortable.
Pikoš platil účet za plyn.
(8 points)E. boiling water
In this problem you are asked to measure the efficienecy of an electric kettle. You can measure the output power by measuring the temperature increase of water in the kettle per unit time. The input power should be written on the bottom of the kettle. Minimalize the error of measurement and describe the methods you used to achieve this. Warning The voltages and currents present are dangerous. Do not use voltmeters and ampermeters without supervision!
(6 points)S. seriálová
- Spiral galaxies can be described using logarithmic spiral$r(φ)=r(0)\exp(φ\tanΦ)$, where $r$ and $φ$ are polar coordinates and Φ is the opening angle, which is an angle between the normal to the vector and the spiral tangent (opening angle increases in the negative direction, in general we use radians and the angle can exceed 2π). Assume Φ = 10$°$. Derive the relation for the ratio of the distances for two neighborings coils of one spiral arm from the galactic centre. How would the ratio change if there were four arms, egually distributed. Write the distance for the neighboring arms for r(0)=8kpc.
- Consider infinite universe with uniform stellar density and no extinction. Write the relation for the integral and differential star counts. What will happen if the apparent magnitude increases a lot?
- *Bonus:** What is the probability that two stars in the galaxy will be projected into one spot? Consider lonely stars, not binaries.
Janapka.