Series 5, Year 29
Upload deadline: -, CET
(2 points)1. let it flow
Thin wire with resistance $R=100mΩ$ and length $l=1\;\mathrm{m}$, that is connected to the source of DC with voltage $U=3V$, contains in its volume $N=10^{22}$ free electrons, which contribute to the electric current. Determine what is the average speed (more accurately net velocity) of these electrons in the wire.
(2 points)2. multiparticular
Let's have a container that is split by imaginary plane into two disjunct parts A and B, identical in size. There are $nparticles$ in the container and each of them has a probability of 50 % to be in part A and probability 50 % to be in part B. Figure out the probabilities of the part A containing $n_{A}=0.6n$ or $n_{A}=1+n⁄2$ particles respectively.. Solve it for $n=10$ and $n=N_{A}$, where $N_{A}≈6\cdot 10^{23}$ is Avogadro's constant.
(3 points)3. egyptian gate
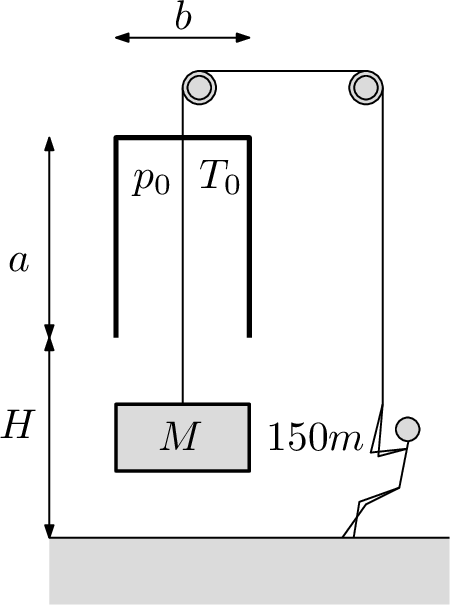
Ancient Egyptians could build a gate, but they hadn't invented the portcullis yet so they closed the gate with nilans (limestone blocks). There are 150 slaves of mass $m=60\;\mathrm{kg}$, who are at the moment slowly opening a gate closed with a nilan of mass $M=8t$. The nilan fits precisely (air-tightly) into a structure above the gate whose inner dimensions are $a=3\;\mathrm{m}$, $b=0.5\;\mathrm{m}$ and $c=3\;\mathrm{m}$. The original pressure inside the structure is $p_{0}=100kPa$ and the original temperature is $T_{0}=300K$. The structure is situated at high $H=3\;\mathrm{m}$ above the ground. Find out how high are the slaves able to lift the nilan, using only their own weight if the air temperature stays constant.
(4 points)4. safe ride
A car is approaching a wall with a trajectory that is perpendicular to the wall. The driver, however, wishes to approach the wall safely. Find the car's speed as a function of time, so that the distance between the car and the wall is, at every moment, the same as the distance the car would travel with its instantaneous speed in $T=2\;\mathrm{s}$.
(5 points)5. rolling stones
There is a sphere with inhomogeneous distribution of density on an inclined plane. We know the angle of inclination of the plane $α$, the radius of the sphere $R$ and the distance $t$ of the centre of mass from its geometrical centre. If we label the centre of the sphere $S$, the point of touch with the plane $D$ and the centre of mass $T$, then we can define the angle $φ_{0}=∠DST$ as the initial angle (before any motion begins). We also know that the centre of mass is situated in a plane given by the line segment $DS$ (the normal to the inclined plane) and the down-sloping direction. Considering all the parameters given, carefully describe the time evolution of the sphere's state of motion. The sphere does not slip.
(5 points)P. underground
As we all know, it is always a little bit chilly in the caves of central Europe, usually about 4 °C. Why, on the other hand, is it always warm in the underground (subway, metro) throughout the whole year? Is more heat produced by the people present or by the technology?
(7 points)E. photographic
With the aid of a digital camera measure the frequency of the AC voltage in the electrical grid. A smart phone with an app supporting manual shutter speed should be a sufficient tool.
(6 points)S. naturally variant
- Use the relation for entropy of ideal gas from the solution of third serial problem
$$S(U, V, N) = \frac{s}{2}n R \ln \left( \frac{U V^{{\kappa} -1}}{\frac{s}{2}R n^{\kappa} } \right) nR s_0$$
and the relation for the change of the entropy
$$\;\mathrm{d} S = \frac{1}{T}\mathrm{d} U \frac{p}{T} \mathrm{d} V - \frac{\mu}{T} \mathrm{d} N$$
to calculate chemical potential as a function of $U$, $VaN$. Modify it further to get the function of $T$, $pandN$.
Hint: The coefficients like 1 ⁄ $T$ in front of d$U$ can be calculated as a partial derivative of $S(U,V,N)$ by $U$. Don't forget that ln$(a⁄b)=\lna-\lnb$ and that $n=N⁄N_{A}$.
Bonus: Express similarly temperature and pressure as functions of $U$, $VandN$. Eliminate the pressure dependence to get the equation of state.
- Is the chemical potential of an ideal gas positive or negative? (Assume $s_{0}$ is negligible.)?
- What will happen with a gas in a piston if the gas is connected to a reservoir of temperature $T_{r}?$ The piston can move freely and there is nothing acting on it from the other side. Describe what happens if we allow only quasistatic processes. How much work can we extract? Is it true that the free energy is minimized?
Hint: To calculate the work, this equation can be useful:
$$\int _{a}^{b} \frac{1}{x} \;\mathrm{d}x = \ln \frac{b}{a}.$$
- We defined the enthalpy as $H=U+pV$ and the Gibb's free energy as $G=U-TS+pV$. What are the natural variables of these two potentials? What other thermodynamic quantities do we obtain by differentiating these potentials by their most natural variables?
- Calculate the change of grandcanonic potential d$Ω$ from its definition $Ω=F-μN$.