Series 5, Year 23
Upload deadline: -, CET
1. photon fountain
Honza is not satisfied with the current bed standard. Thus, he started to test laser levitation. He bought a ball with a perfectly polished mirror surface of mass $m$, radius $r$ and put it on the ground. The ground was immediately lit by the laser with a wave length $\lambda$ and surface power $P$. What is the height of the ball at equilibrium? To get extra points, you may try to solve the problem for a ball made of glass. We suppose, in both the cases, that the laser will not fuse the ball and the experiment takes place in a homogenous gravitational field.
brought by Honza Humplík
2. a spring of Lukáš’
Lukáš found an old sofa spring of force constant $k$, coil radius $r$, length $l$ and the number of coils $n$. Since he was bored, he connected the spring to electric current $I$. How did the action change the force constant of the spring?
Lukáš's idea after Aleš told him to have one
3. a wagon
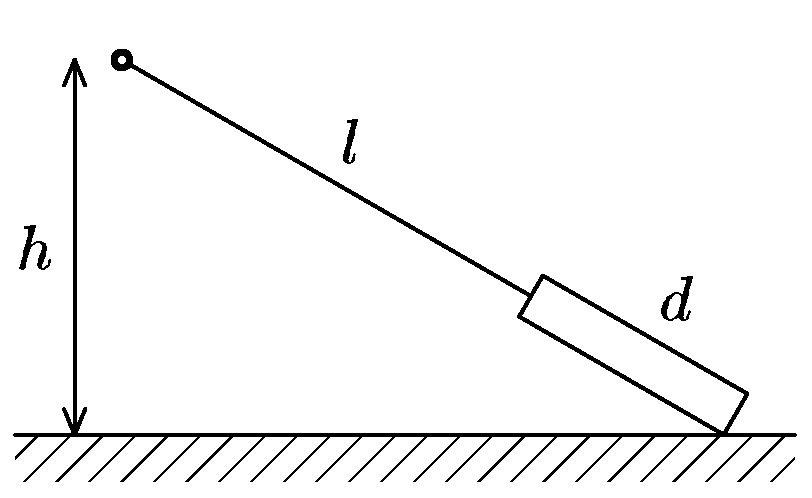
A cord of length $l$ = 1.5 m is tied to a fixed point at height $h$ = 1 m. There is a plank of length $d$ = 0.5 m attached at the end of the cord so that the cord is stretched; the cord and the plank lie in the same line (see picture). On releasing the ties, the plank will slide along its edge before touching the ground with the surface of its bottom side. Then it will move in the direction opposite to the friction force with the friction coefficient $f$. Determine the value of the coefficient so that the plank’s side attached to the cord stops reaching the projection of the fixed point defined beforehand.
thought of as trivial by Lukáš
4. the end of the world
It is a well-known fact that an asteroid hits the Earth on its way around the Sun (it is moving in the same plane as the Earth does) December 21, 2012. Suppose that the asteroid’s orbit is an ellipse with the following parameters: lengths of the transverse (major axis) and conjugate (minor axis) diameter are 4 AU and 0.5 AU respectively. People were far too busy to start solving the problem before December 1, 2012. What is the trajectory that needs to be used by a brave world authority to unleash a nuclear warhead to avert the end of the world?
thanks to Honza Humplík
P. tunelling
Kryštof set on a journey by train and fell asleep. When he woke up in a tunnel, he felt that there is a force dragging him to a side. Although the train was lit up, he could not see outside. He remembered that the train track is tilted at corners. He realised that even though he remembers the original direction of the train he has no clue as to the direction of the corner taken. In other words, he cannot tell the difference between left-turning train being sufficiently slow, the resultant force directed towards the centre of the corner and the right-turning train being fast enough, the resultant force directed out of the corner. Suggest an experiment to help Krystof solve the problem. The more propositions you submit, the more points you get.
by Kryštof from the underground
E. resonance
When you stand in an enclosed space and play a right tone, you can face its resonance frequency. As the resonance frequency depends on the size of the resonator, it can thence be determined. Choose an appropriate room (ideally, a small one with empty walls – e.g. bathroom), measure the frequency and contrast the results.
sang in the bathroom by Jakub Michálek
S. a light in the matter
- The index of refraction in a nonlinear medium varies with the intensity of light $I$ as $n=n_{1}+n_{2}I$, where $n_{1}$ and $n_{2}$ are positive constants. Describe the behaviour of a ray of light of given width passing through this medium, assuming the light intensity decreases as we go from the centre to the edges of the ray. (Qualitative description is acceptable, an analytic model and solution will obtain extra credit.)
- A slab of width $a$ consists of 2$N$ parallel neigbouring slabs (with no gaps) with alternating indices of refraction $n_{1}$ and $n_{1}$. A light wave is incident perpendicularly on the front slab. What is the effective index of refraction of this composite slab for $N→∞?$ Can you think of a physical reason why?
Hint: for any real matrix $A$ <p style=„text-align:center;“> lim_{$N→∞}(I+A/N)^{N}=\exp(A)$,
where $I$ is the identity matrix and exp($A)=I+A+A^{2}/2!+A^{3}/3!+\ldots]$.