Series 6, Year 24
Upload deadline: -, CET
1. warm up
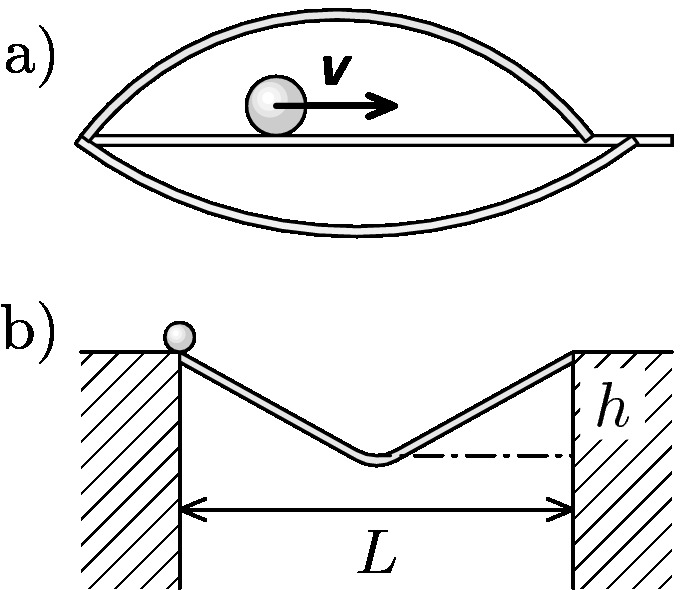
crooked table
Small ball is moving along a horizontal table from one end to the other with some initial velocity. In which case is the time required for the ball to traverse the table the shortest? Explain your choice. - Table has a concave bow. - Table has a convex bow. - Table is flat. - The curvature of the table does not matter.
broken bridge
Small valley of width $L$ is bridged using a board that is broken in the middle. It is however not entirely broken and still holds together so that its shape resembles that of a graph of absolute value. We place a small ball at one end and let it go. What is the appropriate depth of this bridge so that the time required for the ball to get to the other side is the shortest? Assume the ball does not lose energy while rolling over the bridge. You may need to know that the function $f(x) = x+1/x$ has a minimum at $x=1$.
2. evil triangle
Let's have a long slit with a little hole next to it. Describe the interference pattern that you observe on a screen behind this aperture if you illuminate it with coherent light. You can neglect diffraction of light both due to the hole and due to the slit.
3. airplane
How long does it take before the Sun rises and sets as seen from an air-plane that flies in the ecliptic plane? In the same situation how long is a day? What about night? Necessary information like typical height at which air-planes fly can be surely found on the Internet. Answer these questions for an air-plane flying both east and west.
4. the final solution
How would the power of sunlight hitting the Earth in aphelion change if we were to accelerate the Earth in the direction of motion in such a way to extend a year by a week? Estimate the temperature of the Earth in aphelion and perihelion if its heat capacity is almost zero. For simplicity assume that the original trajectory of the Earth was circular (not the case after the velocity boost).
P. the water porter
How much water can be taken out of a swimming pool (in one trial) using only your hair (assume you have a lot of them)?
E. the discworld
Think of as many ways to verify that the Earth is spherical as you can. If you do verify this statement find a way to measure the radius of the Earth.