Series 2, Year 30
Upload deadline: Upload deadline: 29th November 2016 11:59:59 PM, CET
(3 points)1. beach date
Imagine you are going on a date with your girlfriend/boyfriend and you end up watching the sunset on the beach. The sun above the sea horizon looks very romantic, so to prolong this special moment, you decide to use a forklift to lift you up. The forks of the forklift move up with such speed that you can see the sun touching the horizon at any moment. Determine the speed of the forks.
Dominika vzpomínala na Itálii.
(3 points)2. ultra high temperature superconducticvity
Many types of materials, mostly metals, have increasing dependence of resistivity on temperature. However, there are semiconductors or graphite which show a decreasing dependence. And you have also probably heard about superconductivity, the natural phenomenon when a cooled material shows almost no electrical resistance and becomes a perfect conductor. Our current state of knowledge says that the temperature of a superconductor must be well below room temperature, but let's assume that the equation defining the resistance is $R=$ R_{0} (1 + αΔt)$$, where $R_{0}is$ the resistance at room temperature, $αis$ the temperature coefficient of resistance and $Δt$ is the temperature difference with respect to room temperature, and the equation holds for any temperature. Using this equation and coefficients $α_{C}=-0.5\cdot 10^{-3}K^{-1}$ for graphite and $α_{Si}=-75\cdot 10^{-3}K^{-1}$ for silicon, we obtain zero resistance for high temperatures. Determine these two temperatures and explain why the superconducting phenomenon does not work this way, i.e. neither carbon nor silicon are superconductors at high temperatures.
Karel se inspiroval nekonstantními konstantami.
(6 points)3. looping
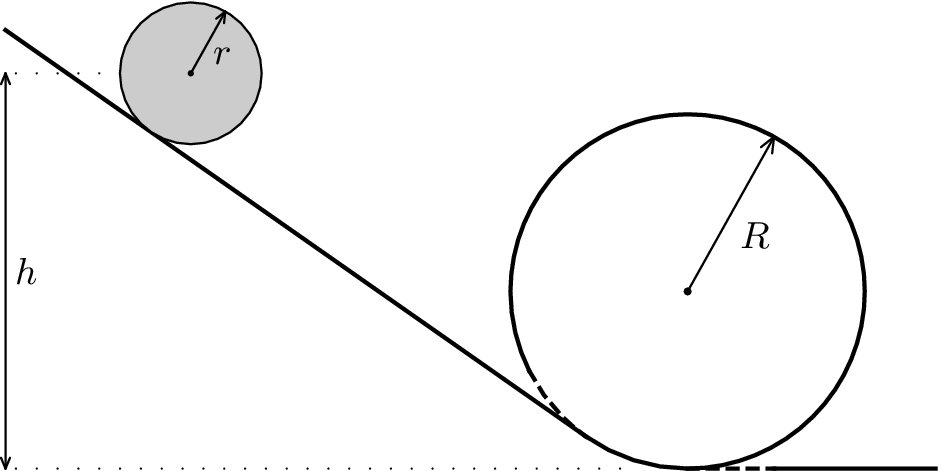
We have a plane inclined at an angle $α$ which is smoothly connected to a loop of radius $R$. What is the minimal initial height $h$ where we have to place a ball of radius $r$ (comparable to $R$, but smaller), so that the ball will roll through the loop? The ball must be always in contact with the plane or the loop and we assume that the ball does not slip.
Kuba přemýšlel nad klasickou úlohou.
(6 points)4. tiny ball
Imagine the motion of a homogeneous ball: it starts with translation (without rotation) and gradually transitions to rolling (without slipping). Determine the time of the transition from pure translation to rolling without slipping. Consider different radius, mass, initial speed and coefficient of friction of the ball.
Lada dělala kotrmelce u zamyslela se u toho.
(7 points)5. tea container problem
We have a tea container with a tap near the bottom and an airtight lid (maybe you know these from your school canteen). Determine the volume of tea we can pour from the tap before we have to open the valve to equalize the pressure in the container.
Lukáše na soustředění trápilo, kolik čaje má být ve várnici.
(9 points)P. an effective machine
Guns can be considered to be heat engines. Calculate the efficiency of a gun, say a pistol or a rifle.
Michal původy svých nápadů raději nesděluje.
(12 points)E. one full fat milk, please
Milk with higher fat content should be „whiter“ – more light is scattered and less is transmitted. Conduct a measurement of the fat content of milk with the help of a color scale (contact us at fykos@fykos.czto get the pdf with the scale – you have to print it yourself). The difference in whiteness is most apparent when you add a dye to each glass of milk. You can use e.g. black ink or any other dye, but with different colors you have to create your own color scale which you have to add to your solution. Use different types of milk and mixture of milk with water. Discuss the reliability of this method of measurement.
Mára byl bledý jako stěna.
(10 points)S. guessing problem
- Describe in your own words the purpose of interval estimation of mean of a normal distribution and explain its physical interpretation (it is sufficient to describe, in your own words, the following concepts: physical interpretation of the estimation of expected value, difference between point and interval estimation, measurement uncertainty). It’s not necessary to state the exact mathematical derivations. It’s sufficient to briefly explain the concepts and their properties.
- Attached to this task, in the file mereni1.csv there are measured values of a certain physical quantity (assume type B uncertainty of B $s\_B = 0{,}1$). Create both the point and interval estimations of the measured physical quantity and try to interpret their meaning.
- Suppose we measure a certain physical quantity and we know that due to the method being used, the measured values will have a variance equal to a constant $c$ (ignore the type B uncertainty). How many measurements do we need to make to achieve an uncertainty below $s$?
- In the attached file mereni2.csv there are data of measurements one physical quantity two different ways (neglect type B uncertainty). Which method used more precise measurement equipment? Which method produced a more precise results Briefly give reasons for your answers.
Bonus: Try to rigorously derive that in a normal distribution the sample variance is an unbiased estimate of the real variance (i.e. the mean of sample variance is equal to the real variance). For the solution of this problem you may use any and all sources (if you cite them correctly).
For data processing and creating the plots, you may use the R programming language. Most of these tasks can be solved by slightly altering the attached scripts.
Michal guessed the optimal wording of the problem, let's hope he was right.