Series 1, Year 28
Upload deadline: -, CET
(2 points)1. consumption of antimatter
How much antimatter would we need to generate enough electricity for the Czech Republic for a year? We have enough matter and we assume that there would be no losses.
Karel was watching Angels and Demons from Dan Brown.
(2 points)2. streaimng streamlines
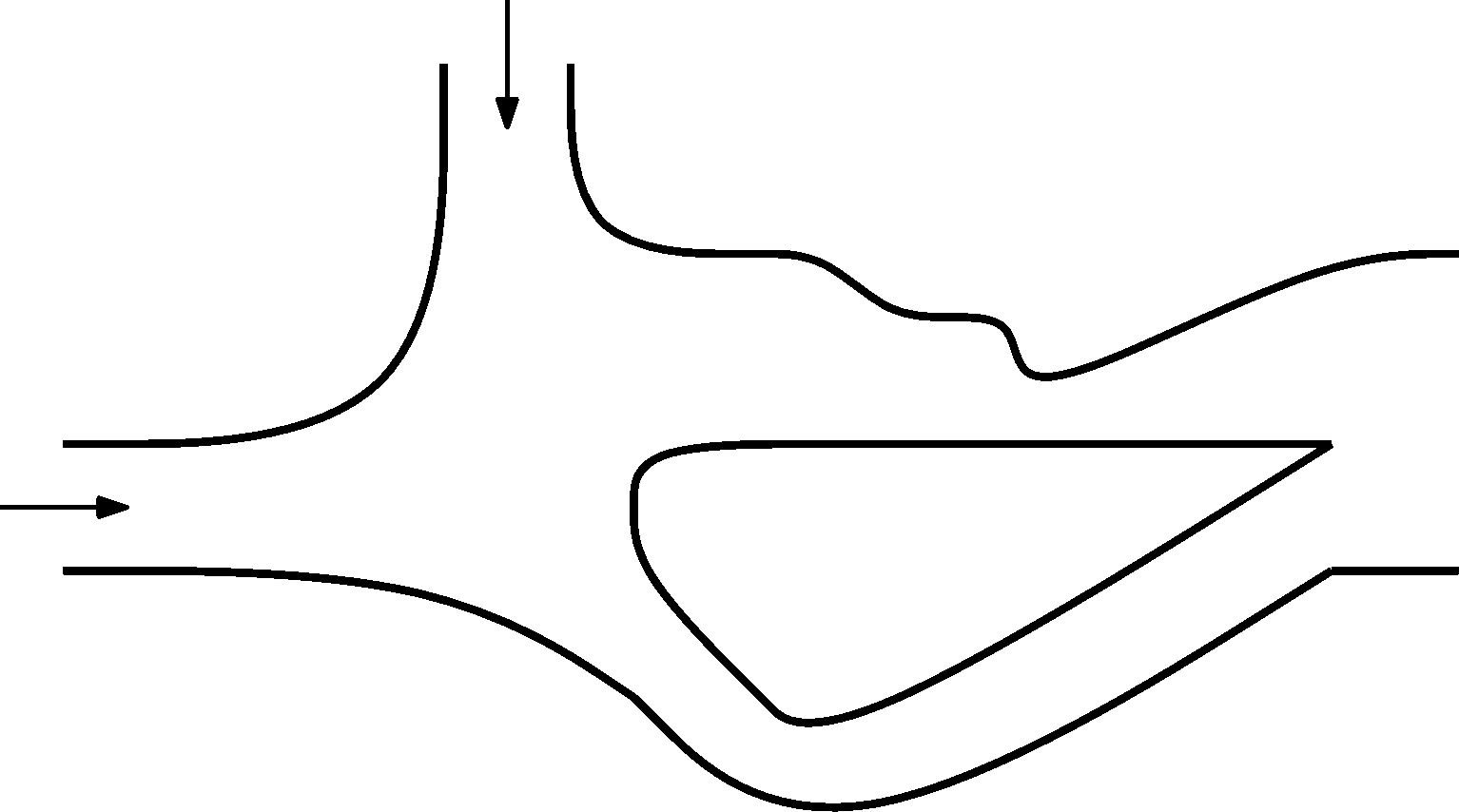
Draw streamlines into the picture. Into both openings with an arrow the same amount of water flows, All the water then flows out through one opening, the third one. The flow is stable and is slow enough that we can consider it not to be turbulent. When drawing follow the rules that dictate the shapes of the streamlines and write these rules down as comments to the picture. We don't expect that this problem will be solved quantitatively. Comment Draw into the bigger picture available from the website.
kolar
(3 points)3. accelerating
Explain why and how the following situations occur:
- In a cistern of a rectangular cuboid shape that is filled with water a ball is floating on the surface of the water. Describe the movement of the ball if the cistern starts moving with a constant acceleration small enough that the water shall not flow over the edge.
- In a cistern of a rectangular cuboid shape that is filled with water a ball filled with water is floating. Describe the movement of the ball if the cistern starts moving with a constant acceleration small enough that the water shall not flow over the edge.
- In a closed bus a ballon is floating near the ceiling. Describe its movement if the bus starts accelerating constantly
Dominika and Pikoš during a physics exam
(4 points)4. doom of the Titanic
Náry always wanted a boat and so one beautiful day he bought himself one in the shape of a cuboid without a top side (like a bath) with outer sides of $a$, $b$, $c$ and with a width of wall of $d$, which was created from scented wood of a density $ρ$ (bigger density than water). The second day he took his boat outfor a ride on the water and he found out that it has a small hole on the bottom through which water flows with a flow rate of $Q_{1}$. That was unfortunate but since he was a man of action he started calculating how long until water starts entering the boat from the top. The same question is asked by this task.Conider also the situation where Náry of a mass $m$ would have sat in the boat and while calculating would spill water out of the boat with a flow rate of $Q_{2}$. The boat is horizontal the whole time.
Kiki heard about the problem that nearly all tasks are thought up by Karel.
(5 points)5. a thousand year old bee
Calculate the power required by a bee to remain in the air and approximate how long a bee that has just eaten can remain in the air for(at a constant altitude).
Michael thought during a discussion about quadcopters.
(5 points)P. Moon from Mars
Can you see the Moon from Mars with a naked eye.Ground your answer in calculations.
Kuba wanted to be brief.
(8 points)E. charged potato
Measure the load characteristic of a potato as a source of electric voltage with electrodes made from different metals.
Karel was thinking about easy experiments.
(6 points)S. Unsure
- Write down the equations for a throw in a homogeneous gravitational field (you don't need to prove them but you need to know how to use them). Design a machine that will throw an item and determine the angle of approach and the velocity. You can throw with the item with a spring, determine its spring constant, mass of the object and calculate the kinetic energy and thus the velocity of the item. What do you think is the precision of the your value of the velocity and angle? Put the boundaries determined by this error into the equations and show in what boundaries we can expect the distance of the landing from the origin to be.Throw the item with your device at least five times and determine the distance of the landing and what are the boundaries within which you are certain of your distance? Show if your results fit into your predictions. (For a link to video with a throw you get a bonus point!)
- Tie a pendulum with an amplitude of $x$, which effectively oscillates harmonically but the frequency of its oscillations depends on the maximum displacement $x_{0}$
$$x(t) = x_0 \cos\left[\omega(x_0) t\right]\,, \quad \omega(x_0) = 2\pi \left(1 - \frac{x_0^2}{l_0^2}\right)\,,$$
where $l_{0}is$ some length scale. We think that are letting go of the pendulum from $x_{0}=l_{0}⁄2$ but actually it is from $x_{0}=l_{0}(1+ε)⁄2$. B By how much does the argument of the cosine differ from 2π after one predicted period? How many periods will it take for the pendulum to displaced to the other side than which we expect? Tip Argument of the cosine will in that moment differ from the expected one by more than π ⁄ 2.
- Take a pen into your hand and let it stand on its tip on the table. Why does it fall? And what will determine if it will fall to the right or to the left? Why can't you predict a die throw even though the laws of physics should predict it? When you play billiard is the inability to finish the game only due to being incapable of doing all the neccessary calculations? Write down your answers and try to enumerate physics phenomenons that occur in daily life which are unpredictable even if we know the situation well.