Series 1, Year 22
Upload deadline: -, CET
1. sliding and oscillations
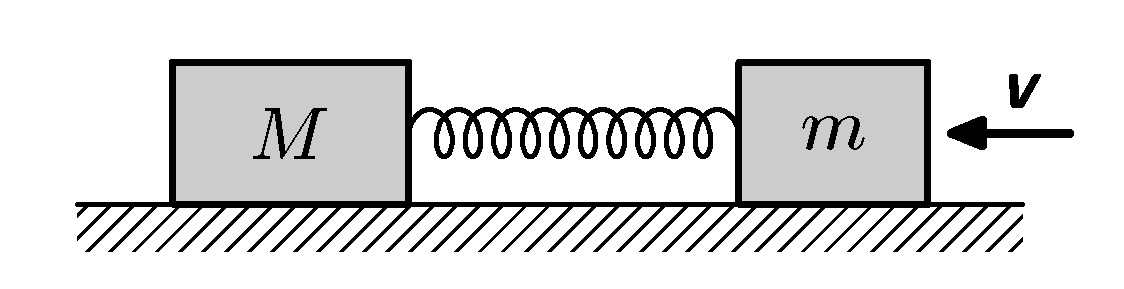
Two weights of masses $m$ and $M$ are connected by a spring of stiffness $k$ and lies on flat smooth surface (friction can be neglected). Body of mass $m$ gets velocity $\textbf{v}$ (see picture). What will be the smallest distance between the bodies? And when it will be reached?
V ročenkách kanadské FO našel Honza Prachař.
2. pirate and golden reward
One pirate should get 10 golden coins. However the captain does not want to give money so easily and melts the gold to a cylinder shape. And together prepares similar cylinder, made from brass with identical dimensions. Because the golden cylinder has inside some air, both weight the same. What is the best way to select the golden cylinder?
Úlohu vymyslel kolega Mirka Beláňe.
3. do not cradle me
Kathy is on a swing (a plank suspended on 2 ropes). At high displacements she kneels down, in lowest point she gets up. This movements she periodically repeats. Ration of distance of centre of gravity from the rotation axis at kneeling down and at standing is 2^{1 ⁄ 12} ≈ 1,06. How many times Kathy must swing to double the amplitude of swinging?
Z asijské olympiády přinesl Honza Prachař
4. something for motorists
At dangerous curves and crossings you often see a convex mirror. It is distorting real picture, such as distances and velocities are unreal. Assume our distance from the mirror is $d$, distance of incoming car from the mirror is $L$, its real velocity is $v$ and mirror diameter is $R$.
Based on the image in mirror, how far do we see the car? What is its apparent speed? How different is time it enters the crossing, calculated based on data from image, compared to reality? Assume some concrete values for all parameters and evaluate, if this difference can be significant.
Při cestě na soustředění zažil Marek Scholz.
P. Copernicus versus Ptolemaios

Ptolemaios's geocentric model
The year 2009 is international year of astronomy and remembers 400 years from discovering telescope. Lets go back 400 years to the times, when the telescope was already invented, but the classical physics was just in its beginnings. At this time there were two explanation of world: Copernicus's heliocentric and Ptolemaios's geocentric. Design an experiment, which will be able to decide which of above models is correct. Document, what results you can expect and how you can interpret it. You do not have to make the observation itself. Explain, why in geocentric model the Sun and Earth are connected by a line.
Významný důkaz chtěl připomenout Pavel Brom.
E. what is smelling here?
Measure difference of density of fresh and spoiled egg and find out its time dependence! Assume statistical approach.
Hint: Eggs get spoiled very quickly if exposed to sun light and heat.
S. equivalence principle
- What had to be a conditions for Galileo to fail its experiment? Leaning tower in Pisa is $h=55\;\mathrm{m}$ high. Assume that both balls have the same diameter $R=8\;\mathrm{cm}$ and that one is made from lead of density $ρ=11300\;\mathrm{kg}\cdot \mathrm{m}^{-3}$. What density must be the second ball to achieve the difference in time of impact to be bigger than $ΔT=0,3s?$
- What is precision of original Eötvös measurement of equality of gravitational and inertial mass for neutrons and protons, if in wood neutrons make 50 percent of mass and in platinum 60 percent of mass? Neglect mass of electrons and binding energy.
- Verify the assumption, that in Budapest is $g_{s}′$ negligible comparing to $g$.
Zadali autoři seriálu Jakub Benda a Pavel Motloch.